题目内容
育英学校派出5名优秀教师去边远地区的三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有( )
| A、80种 | B、90种 |
| C、120种 | D、150种 |
考点:排列、组合的实际应用
专题:应用题,排列组合
分析:分组法是(1,1,3),(1,2,2)共有25种,再分配,共有A33种果,根据分步计数原理知结果.
解答:
解:依题意分组法是(1,1,3),(1,2,2)共有
+
=25,
再分配,乘以A33,即得总数150,
故选:D.
| ||||||
|
| ||||||
|
再分配,乘以A33,即得总数150,
故选:D.
点评:本题考查分步计数原理,首先分组,再进行排列,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知实数x,y满足不等式组
,则目标函数z=3x-4y的最小值m与最大值M的积为( )
|
| A、-60 | B、-48 |
| C、-80 | D、36 |
如果loga8>logb8>0,那么a、b间的关系是( )
| A、0<a<b<1 |
| B、1<a<b |
| C、0<b<a<1 |
| D、1<b<a |
设m、n是两条不同的直线,α、β是两个不同的平面.下列四个命题中,正确的是( )
| A、α∥β,m?α,n?β,则m∥n |
| B、α⊥β,m⊥β,则m∥α或m?α |
| C、α⊥β,m?α,n?β,则m⊥n |
| D、α∥β,m⊥β,n⊥α,则m∥n |
设正项等比数列{an}的前n项和为Sn,公比为q,若Sk-2=3,Sk=15,Sk+2=63,则q=( )
| A、-2 | B、2 | C、-4 | D、4 |
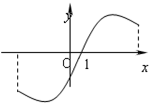 若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中
若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中 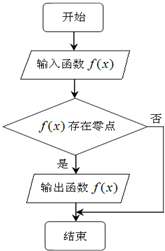 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|,则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|,则输出的函数的个数为( )