题目内容
平面向量的集合A到A的映射f(
)=
-(
•
)
,其中
为常向量.若映射f满足f(
)•f(
)=
•
对任意的
,
∈A恒成立,则
的坐标可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
A、(
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据已知,将f(
)•f(
)=
•
利用映射关系式代替,得到关于
的等式解之.
| x |
| y |
| x |
| y |
| a |
解答:
解:∵f(
)=
-(
•
)
,其中
为常向量.
∴f(
)•f(
)=
•
=[
-(
•
)
]•[
-(
•
)
],
整理得,2
•
=
•
•
2,
∴
2=2,
从四个选项中选择
的模平方为2的选项,
对于A,向量的模的平方为
;对于B,向量的模的平方为2;对于C,对于向量的模的平方
;
对于D,向量的模的平方为
.
故选B.
| x |
| x |
| x |
| a |
| a |
| a |
∴f(
| x |
| y |
| x |
| y |
| x |
| x |
| a |
| a |
| y |
| y |
| a |
| a |
整理得,2
| y |
| •a |
| x |
| a |
| x |
| a |
| y |
| a |
| a |
∴
| a |
从四个选项中选择
| a |
对于A,向量的模的平方为
| 1 |
| 4 |
| 5 |
| 8 |
对于D,向量的模的平方为
| 31 |
| 16 |
故选B.
点评:本题考查了向量的数量积的运算.

练习册系列答案
相关题目
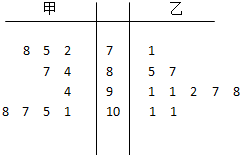 两名射击运动员甲、乙在某次比赛中的成绩(单位:环)用茎叶图表示如图,甲、乙两人射击成绩的中位数分别用n甲、n乙表示,则( )
两名射击运动员甲、乙在某次比赛中的成绩(单位:环)用茎叶图表示如图,甲、乙两人射击成绩的中位数分别用n甲、n乙表示,则( )| A、n甲>n乙 |
| B、n甲<n乙 |
| C、n甲=n乙 |
| D、n甲、n乙的大小关系不确定 |
4月20日四川庐山发生7.0级,某地区医疗队知道此消息后准备从5个内科医生和4个外科医生中选派5人去参加救援,其中外科医生至少要派3人参加,则一共有( )种选派方法.
| A、126 | B、80 | C、60 | D、45 |
已知f1(x)=sinx-cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2013(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
在极坐标系中,圆C的圆心为(6,
),半径为5,直线θ=α(0≤α≤
,ρ∈R)被圆截得的弦长为8,则α的值为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
极坐标方程4ρsin2
=5表示的曲线为( )
| θ |
| 2 |
| A、直线 | B、圆 | C、椭圆 | D、抛物线 |
用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4的值时,第一步算的是( )
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
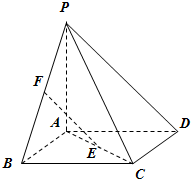 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证: