题目内容
平面上有9个点,其中4个点在同一条直线上,此外任三点不共线.
(1)分别以其中两点为起点和终点,最多可作出几个向量?
(2)过每两点连线,可得几条直线?
(3)以每三点为顶点作三角形可作几个?
(1)分别以其中两点为起点和终点,最多可作出几个向量?
(2)过每两点连线,可得几条直线?
(3)以每三点为顶点作三角形可作几个?
考点:计数原理的应用
专题:排列组合
分析:(1)向量具有方向和大小的,分三类,一类两点全在直线上,一类在一直线上4点任取一点,直线外再取一点,另一类在一直线上4点不取,直线外取两点即可,根据分类计数原理可得.
(2)分三类,一类两点全在直线上,一类在一直线上4点任取一点,直线外再取一点,另一类在一直线上4点不取,直线外取两点即可根据分类计数原理可得.
(3)分三类,第一类,在同一条直线上4个点选一个,再另外的5个点选2个,第二类,在同一条直线上4个点选2个,再另外的5个点选1个,第二类,在另外的5个点选3个,根据分类计数原理可得
(2)分三类,一类两点全在直线上,一类在一直线上4点任取一点,直线外再取一点,另一类在一直线上4点不取,直线外取两点即可根据分类计数原理可得.
(3)分三类,第一类,在同一条直线上4个点选一个,再另外的5个点选2个,第二类,在同一条直线上4个点选2个,再另外的5个点选1个,第二类,在另外的5个点选3个,根据分类计数原理可得
解答:
解:(1)第一类,起点和终点分别属于同一直线的4个点中的2个点,有
=12种,
第二类,起点和终点分别属于同一直线的4个点的一个点,另一个点在直线的5个点中的一个,2×4×5=40种,
第三类,起点和终点分别属于直线的5个点中的两个,
=20种,
根据分类计数原理得,12+40+20=72个向量
(2)解:第一类,在一直线上4点任取两点构成同一直线,1条,
第二类,在一直线上4点任取一点,直线外再取一点可构成4×5=20条
第三类,在一直线上4点不取,直线外取两点可构成
=10条,
根据分类计数原理得,故一共1+20+10=31条,
(3)分两类,第一类,在同一条直线上4个点选一个,再另外的5个点选2个,有
•
=40个,
第二类,在同一条直线上4个点选2个,再另外的5个点选1个,有
•
=30个,
第二类,在另外的5个点选3个,有
=10个,
根据分类计数原理得,以每三点为顶点作三角形可作40+30+10=80个.
| A | 2 4 |
第二类,起点和终点分别属于同一直线的4个点的一个点,另一个点在直线的5个点中的一个,2×4×5=40种,
第三类,起点和终点分别属于直线的5个点中的两个,
| A | 2 5 |
根据分类计数原理得,12+40+20=72个向量
(2)解:第一类,在一直线上4点任取两点构成同一直线,1条,
第二类,在一直线上4点任取一点,直线外再取一点可构成4×5=20条
第三类,在一直线上4点不取,直线外取两点可构成
| C | 2 5 |
根据分类计数原理得,故一共1+20+10=31条,
(3)分两类,第一类,在同一条直线上4个点选一个,再另外的5个点选2个,有
| C | 1 4 |
| C | 2 5 |
第二类,在同一条直线上4个点选2个,再另外的5个点选1个,有
| C | 2 4 |
| C | 1 5 |
第二类,在另外的5个点选3个,有
| C | 3 5 |
根据分类计数原理得,以每三点为顶点作三角形可作40+30+10=80个.
点评:本题主要考查了分类计数原理,如何分类时关键,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
下列命题是假命题的是( )
| A、若x2+y2=0,则x=y=0 |
| B、若a+b是偶数,则a,b都是偶数 |
| C、矩形的对角线相等 |
| D、余弦函数是周期函数 |
已知在二面角α-l-β的α面上有Rt△ABC,斜边BC在l上,A在β面上的射影为D,∠ABD为θ1,∠ACD为θ2,二面角α-l-β为θ.请问以下条件哪一个成立( )
| A、sin2θ=sin2θ1+sin2θ2 |
| B、cos2θ=cos2θ1+cos2θ2 |
| C、tan2θ=tan2θ1+tan2θ2 |
各项均不为0的等差数列{an}中,若an2-an-1-an+1=0(n∈N*,n≥2),Sn为数列的前n项和,则S2012=( )
| A、0 | B、2011 |
| C、2012 | D、4024 |
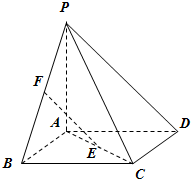 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
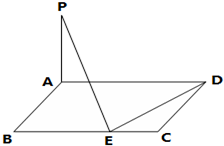 (理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.
(理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.