题目内容
若x∈R，则函数y=|x|+
的最大值是 ．
| 2-x2 |
考点：函数的最值及其几何意义
专题：转化思想
分析：将函数解析式平方，再利用二次函数求最值．
解答：
解：∵y2=2+2|x|•
=2+2
≤4，
∴y≤2．当且仅当x=±1时，y取得最大值2，
故答案为：2．
| 2-x2 |
| -(x2-1)2+1 |
∴y≤2．当且仅当x=±1时，y取得最大值2，
故答案为：2．
点评：本题考查了二次函数的最值问题，将函数解析式转化为二次函数形式是求最值的一种重要的方法．
练习册系列答案
相关题目
一个几何体的正视图和俯视图如图所示，其中俯视图是一个圆内切于一个正三角形，则该几何体的侧视图的面积为某几何体的三视图如图所示，则该几何体的表面积为（ ）
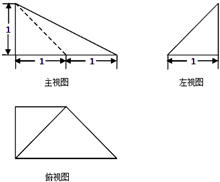
A、3+
| ||||||||
B、3+
| ||||||||
C、3+
| ||||||||
D、
|