题目内容
已知复数z=lg（x2-1）+ilg（x-1）（其中i是虚数单位），若z在复平面上对应的点位于第三象限，则实数x的取值范围是 ．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：利用复数z=lg（x2-1）+ilg（x-1）在复平面上对应的点位于第三象限，可得得
，解此不等式组即可求得实数x的取值范围．
|
解答：
解：依题意，得
⇒
⇒
，
解得：1＜x＜
．
∴实数x的取值范围是（1，
）．
故答案为：（1，
）．
|
|
|
解得：1＜x＜
| 2 |
∴实数x的取值范围是（1，
| 2 |
故答案为：（1，
| 2 |
点评：本题考查复数的代数表示法及其几何意义，着重考查对数的运算性质与解不等式的运算能力，属于中档题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
用min{a，b）表示a，b两数中的最小值．若函数f（x）=min{|x|，|x+t|}-
恰有三个零点，则t的值为（ ）
| 1 |
| 2 |
| A、-2 | B、2 |
| C、2或-2 | D、1或-l |
下列函数既是奇函数，又在区间（-1，1）内是减函数的是（ ）
| A、f（x）=-|x| |
| B、f（x）=lg（1-x）-lg（1+x） |
| C、f（x）=2x+2-x |
| D、f（x）=-x3sin2x |
某几何体的三视图如图所示，则该几何体的表面积为（ ）
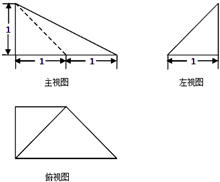
A、3+
| ||||||||
B、3+
| ||||||||
C、3+
| ||||||||
D、
|
集合A={y|y=lgx，x＞1}，B={-3，-2，-1，0，1，2，3，4}，则（∁RA）∩B等于（ ）
| A、{-3，-2，-1，0} |
| B、（-∞，0） |
| C、（0，+∞） |
| D、{-3，-2，-1} |