题目内容
在△ABC中，若c2-ab=a2+b2，则∠C=（ ）
| A、60° | B、90° |
| C、120° | D、150° |
考点：余弦定理
专题：三角函数的求值
分析：利用余弦定理表示出cosC，将已知等式变形后代入求出cosC的值，即可确定出C的度数．
解答：
解：∵在△ABC中，c2-ab=a2+b2，即a2+b2-c2=-ab，
∴cosC=
=-
，
则C=120°．
故选：C．
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
则C=120°．
故选：C．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
下列函数既是奇函数，又在区间（-1，1）内是减函数的是（ ）
| A、f（x）=-|x| |
| B、f（x）=lg（1-x）-lg（1+x） |
| C、f（x）=2x+2-x |
| D、f（x）=-x3sin2x |
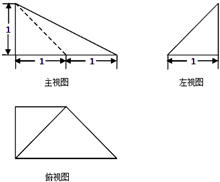
某几何体的三视图如图所示，则该几何体的表面积为（ ）
A、3+
| ||||||||
B、3+
| ||||||||
C、3+
| ||||||||
D、
|
已知sinθ-cosθ=
，则sin2θ的值是（ ）
| 1 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
下列说法正确的是（ ）
| A、任何事件的概率总是在（0，1）之间 |
| B、频率是客观存在的，与试验次数无关 |
| C、随着试验次数的增加，频率一般会越来越接近概率 |
| D、概率是随机的，在试验前不能确定 |
若当P（m，n）为圆x2+（y-1）2=1上任意一点时，等式m+n+c=0恒成立，则c的取值范围是（ ）
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|