题目内容
已知非零向量
，
满足（
-2
）⊥
，（
-2
）⊥
，则向量
与向量
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：数量积表示两个向量的夹角,数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由（
-2
）⊥
，（
-2
）⊥
，算出
•
=
=
，|
|2=|
|2，
再由平面向量的夹角公式，即可算出向量
与向量
的夹角大小．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
| ||
| 2 |
|
| ||
| 2 |
| a |
| b |
再由平面向量的夹角公式，即可算出向量
| a |
| b |
解答：
解：由(
-2
)⊥
，得(
-2
)•
=0，即
2=|
|2=2
•
，
又由(
-2
)⊥
，可得
2=|
|2=2
•
，
所以有
•
=
=
，|
|2=|
|2，
设向量
与向量
的夹角为θ（θ∈[0，π]），
则有cosθ=
=
=
，
所以θ=
，
故选：C．
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| a |
| a |
| b |
又由(
| b |
| a |
| b |
| b |
| b |
| a |
| b |
所以有
| a |
| b |
|
| ||
| 2 |
|
| ||
| 2 |
| a |
| b |
设向量
| a |
| b |
则有cosθ=
| ||||
|
|
| ||||
|
|
| 1 |
| 2 |
所以θ=
| π |
| 3 |
故选：C．
点评：本题考查向量的数量积运算及其向量的夹角公式等知识．
练习册系列答案
相关题目
下列函数既是奇函数，又在区间（-1，1）内是减函数的是（ ）
| A、f（x）=-|x| |
| B、f（x）=lg（1-x）-lg（1+x） |
| C、f（x）=2x+2-x |
| D、f（x）=-x3sin2x |
某几何体的三视图如图所示，则该几何体的表面积为（ ）
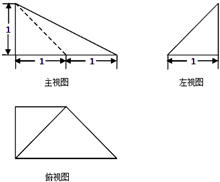
A、3+
| ||||||||
B、3+
| ||||||||
C、3+
| ||||||||
D、
|
已知sinθ-cosθ=
，则sin2θ的值是（ ）
| 1 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
将参加冬季越野跑的600名选手编号为：001，002，…，600．采用系统抽样方法抽取一个容量为50的样本，把编号分50组后，在第一组的001到012这12个编号中随机抽得的号码为004．这600名选手分别穿着三种颜色的衣服，从001到311穿红色衣服，从312到496穿白色衣服，从497到600穿黄色衣服．若从样本中任意抽取一个，则抽到穿白色衣服的选手的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是（ ）
| A、任何事件的概率总是在（0，1）之间 |
| B、频率是客观存在的，与试验次数无关 |
| C、随着试验次数的增加，频率一般会越来越接近概率 |
| D、概率是随机的，在试验前不能确定 |
集合A={y|y=lgx，x＞1}，B={-3，-2，-1，0，1，2，3，4}，则（∁RA）∩B等于（ ）
| A、{-3，-2，-1，0} |
| B、（-∞，0） |
| C、（0，+∞） |
| D、{-3，-2，-1} |
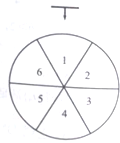商场销售的某种饮品每件售价36元，成本为20元．对该饮品进行促销；顾客每购买一件，当即连续转动三次如图所示转盘，每次停止后指针指向一个数字，若三次指向同一个数字，获一等奖；若三次指向的数字是连号（不考虑顺序），获二等奖；其它情况无奖．