题目内容
若θ是第四象限角,且sin
<0,则
∈ .
| θ |
| 2 |
| θ |
| 2 |
考点:三角函数线
专题:计算题,三角函数的求值
分析:利用象限角的表示方法,即可得出结论.
解答:
解:由题意,θ∈(2kπ-
,2kπ)(k∈Z),
∴
∈(kπ-
,kπ)(k∈Z),
∵sin
<0,
∴
∈(2nπ-
,2nπ)(n∈Z),
故答案为:(2nπ-
,2nπ)(n∈Z)
| π |
| 2 |
∴
| θ |
| 2 |
| π |
| 4 |
∵sin
| θ |
| 2 |
∴
| θ |
| 2 |
| π |
| 4 |
故答案为:(2nπ-
| π |
| 4 |
点评:本题考查象限角的表示方法,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
双曲线
-
=1的左右焦点为F1,F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
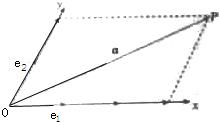 如图,设Ox、Oy是平面内相交成60°角的两条数轴,
如图,设Ox、Oy是平面内相交成60°角的两条数轴,
 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.