题目内容
双曲线
-
=1的左右焦点为F1,F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:依题意,抛物线y2=2bx 的焦点F(
,0),由 (
+c):(c-
)=5:3,可得c=2b,结合双曲线的性质即可求得此双曲线的离心率.
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
解答:
解:∵抛物线y2=2bx的焦点F(
,0),
线段F1F2被抛物线y2=2bx 的焦点分成5:3的两段,
∴(
+c):(c-
)=5:3,∴c=2b,
∴c2=a2+b2=a2+
c2,
∴
=
.
∴此双曲线的离心率e=
=
.
故选B.
| b |
| 2 |
线段F1F2被抛物线y2=2bx 的焦点分成5:3的两段,
∴(
| b |
| 2 |
| b |
| 2 |
∴c2=a2+b2=a2+
| 1 |
| 4 |
∴
| c2 |
| a2 |
| 4 |
| 3 |
∴此双曲线的离心率e=
| c |
| a |
2
| ||
| 3 |
故选B.
点评:本题考查双曲线的简单性质与抛物线的简单性质,求得c=2b是关键,考查分析与运算能力,属于基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
P是双曲线
-
=1(a>0,b>0)的右支上的一点,F1,F2分别是左、右焦点,则△PF1F2的内切圆圆心的横坐标为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、a | ||
| B、b | ||
C、
| ||
D、a+b-
|
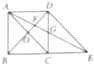 对于向量
对于向量| PAi |
| PA1 |
| PA2 |
| PAn |
| A、点A,C的“平衡点”必为点O |
| B、点D,C,E的“平衡点”为线段DE的中点 |
| C、点A,F,G,E的“平衡点”存在且唯一 |
| D、点A,B,E,D的“平衡点”必在点F |
已知复数(1+i)(a+bi)=2+4i(a,b∈R),函数f(x)=2sin(ax+
)+b图象的一个对称中心是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(
|
函数f(x)=
的图象大致是图中的( )
| cos(πx) |
| x2 |
A、 |
B、 |
C、 |
D、 |
