题目内容
 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.(Ⅰ)求直方图中x的值;
(Ⅱ)试估计所抽取的数学成绩的平均数;
(Ⅲ)试根据样本估计“该校高一学生期末数学考试成绩≥70”的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由频率分布直方图的高之和为组距分之一,即可得到结论;
(Ⅱ)根据频率分布直方图中的数据,求出数据的平均数即可;
(Ⅲ)右面三个举行的面积即为所求.
(Ⅱ)根据频率分布直方图中的数据,求出数据的平均数即可;
(Ⅲ)右面三个举行的面积即为所求.
解答:
解:(Ⅰ)由频率分布直方图的各高之和为组距分之一,
所以(0.012+0.016+0.018+0.024+x)×10=1,
解得x=0.03;
(Ⅱ)根据频率分布直方图中的数据,
得该次数学考试的平均分为
=55×0.012×10+65×0.018×10
+75×0.03×10+85×0.024×10
+95×0.016×10=76.4;
(Ⅲ)根据题意可得:P=1-(0.012+0.018)×10=0.7
故“该校高一学生期末数学考试成绩≥70”的概率为0.7.
所以(0.012+0.016+0.018+0.024+x)×10=1,
解得x=0.03;
(Ⅱ)根据频率分布直方图中的数据,
得该次数学考试的平均分为
. |
| x |
+75×0.03×10+85×0.024×10
+95×0.016×10=76.4;
(Ⅲ)根据题意可得:P=1-(0.012+0.018)×10=0.7
故“该校高一学生期末数学考试成绩≥70”的概率为0.7.
点评:本题考查利用频率分布直方图求众数以及古典概型的概率问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
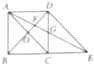 对于向量
对于向量| PAi |
| PA1 |
| PA2 |
| PAn |
| A、点A,C的“平衡点”必为点O |
| B、点D,C,E的“平衡点”为线段DE的中点 |
| C、点A,F,G,E的“平衡点”存在且唯一 |
| D、点A,B,E,D的“平衡点”必在点F |
已知复数(1+i)(a+bi)=2+4i(a,b∈R),函数f(x)=2sin(ax+
)+b图象的一个对称中心是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(
|
 如图,设O是?ABCD所在平面外的任一点,已知
如图,设O是?ABCD所在平面外的任一点,已知