题目内容
10.一程序框图如图所示,如果输出的函数值在区间[1,2]内,那么输入实数x的取值范围是( )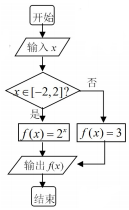
| A. | (-∞,0) | B. | [-1,0] | C. | [1,+∞) | D. | [0,1] |
分析 模拟程序框图的运行过程,得出该程序运行输出的是什么,由此得出解答来.
解答 解:根据题意,得
当x∈[-2,2]时,f(x)=2x,
∴1≤2x≤2,
∴0≤x≤1;
当x∉[-2,2]时,f(x)=3,不符合,
∴x的取值范围是[0,1].
故选:D.
点评 本题考查了程序框图的应用问题,也考查了分段函数的应用问题,解题时应模拟程序框图的运行过程,以便正确解答问题,是基础题.

练习册系列答案
相关题目
20. 已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )
已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )
 已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )
已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}(\vec b+\vec c-\vec a)$ | B. | $\frac{1}{2}(\vec a+\vec b-\vec c)$) | C. | $\frac{1}{2}(\vec a-\vec b+\vec c)$ | D. | $\frac{1}{2}(\vec c-\vec a-\vec b)$ |
1.一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
| A. | 29 000元 | B. | 31 000元 | C. | 38 000元 | D. | 45 000元 |
18.“函数y=f(x)在R上单调递增”是“f'(x)≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知命题p:?c>0,使方程x2-x+c=0有解,则¬p为( )
| A. | ?c>0,方程x2-x+c=0无解 | B. | ?c≤0,方程x2-x+c=0有解 | ||
| C. | ?c>0,使方程x2-x+c=0无解 | D. | ?c≤0,使方程x2-x+c=0有解 |
20.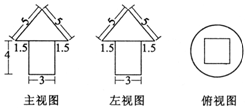 如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )
如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )
 如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )
如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )| A. | (10π+36)cm3 | B. | (11π+35)cm3 | C. | (12π+36)cm3 | D. | (13π+34)cm3 |
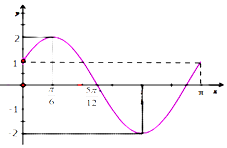 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.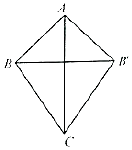 如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.
如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.