题目内容
1.一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )| A. | 29 000元 | B. | 31 000元 | C. | 38 000元 | D. | 45 000元 |
分析 分别设出甲乙两种肥料的车皮数,根据两种原料必须同时够用列出不等式组,得到线性约束条件,列出利润与甲乙两种肥料车皮数的函数,利用线性规划知识求得利润的最大值.
解答 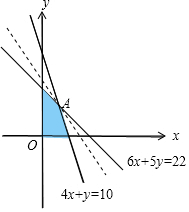 解:设x、y分别表示计划生产甲、乙两种肥料的车皮数.
解:设x、y分别表示计划生产甲、乙两种肥料的车皮数.
由题意,得$\left\{\begin{array}{l}{4x+y≤10}\\{18x+15y≤66}\\{x≥0}\\{y≥0}\end{array}\right.$.
工厂的总利润z=12000x+7000y
由约束条件得可行域如图,
由$\left\{\begin{array}{l}{4x+y=10}\\{18x+15y=66}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
所以最优解为A(2,2),
则当直线12000x+7000y-z=0过点A(2,2)时,
z取得最大值为:38000元,即生产甲、乙两种肥料各2车皮时可获得最大利润.
故选:C.
点评 本题考查了根据实际问题选择函数模型,考查了线性规划知识,解答的关键是确定最优解,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
| A. | 264 | B. | 72 | C. | 266 | D. | 274 |
16.已知集合A={x|x2-6x+5≤0},B={x|2x≥4},则A∩B=( )
| A. | {x|2≤x≤6} | B. | {x|2≤x≤5} | C. | {x|2<x<5} | D. | {x|1≤x≤2} |
10.一程序框图如图所示,如果输出的函数值在区间[1,2]内,那么输入实数x的取值范围是( )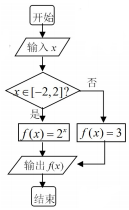

| A. | (-∞,0) | B. | [-1,0] | C. | [1,+∞) | D. | [0,1] |
11.运行如图所示的算法框图,则输出的结果S为( )


| A. | $\frac{1}{2}$ | B. | 0 | C. | -1 | D. | $-\frac{3}{2}$ |
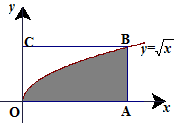 如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.
如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$. 已知全集U=R,集合A=$\left\{{x\left|{y=\sqrt{{x^2}-4x+3}}\right.}\right\}$,B={y|y=log2x,4<x<16},
已知全集U=R,集合A=$\left\{{x\left|{y=\sqrt{{x^2}-4x+3}}\right.}\right\}$,B={y|y=log2x,4<x<16},