题目内容
20．
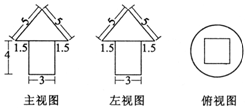如图是一个几何体的三视图，尺寸如图所示，（单位：cm），则这个几何体的体积是（ ）| A． | （10π+36）cm3 | B． | （11π+35）cm3 | C． | （12π+36）cm3 | D． | （13π+34）cm3 |
分析 由三视图可知：该几何体是一个由上下两部分组成的几何体，其中上面是一个圆锥，底面半径为3，高为4；下面是一个棱长分别为3，3，4的长方体．．据此即可得出体积．
解答 解：由三视图可知：该几何体是一个由上下两部分组成的几何体，其中上面是一个圆锥，底面半径为3，高为4；下面是一个棱长分别为3，3，4的长方体．
因此该几何体的体积V=$\frac{1}{3}•π•9•4+3•3•4$=（12π+36）cm3．
故选C．
点评 由三视图正确恢复原几何体即熟练掌握台体和柱体的体积计算公式是解题的关键．
练习册系列答案
相关题目
10．一程序框图如图所示，如果输出的函数值在区间[1，2]内，那么输入实数x的取值范围是（ ）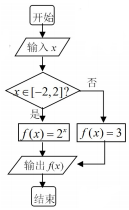
| A． | （-∞，0） | B． | [-1，0] | C． | [1，+∞） | D． | [0，1] |
11．运行如图所示的算法框图，则输出的结果S为（ ）
| A． | $\frac{1}{2}$ | B． | 0 | C． | -1 | D． | $-\frac{3}{2}$ |
8．一个路口的红绿灯，红灯的时间为30秒，黄灯的时间为5秒，绿灯的时间为40秒，当你到达路口时，看见的不是红灯的概率是（ ）
| A． | $\frac{1}{15}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{8}{15}$ |
5．已知命题“?x∈R，使4x2+（a-2）x+$\frac{1}{4}$≤0”是假命题，则实数a的取值范围是（ ）
| A． | （-∞，0） | B． | [0，4] | C． | [4，+∞） | D． | （0，4） |
12．方程$（x+y-2）\sqrt{{x^2}+{y^2}-9}=0$表示的曲线是（ ）
| A． | 一条直线和一个圆 | B． | 一条直线和半个圆 | ||
| C． | 两条射线和一个圆 | D． | 一条线段和半个圆 |
10．已知双曲线的一个焦点坐标为（0，2），它的渐近线方程为y=±$\sqrt{3}$x，则该双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{3}$-y2=1 | B． | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C． | $\frac{{y}^{2}}{3}$-x2=1 | D． | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{2}$=1 |