题目内容
20. 已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )
已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且$\overrightarrow{OA}$=$\vec a$,$\overrightarrow{OB}$=$\vec b$,$\overrightarrow{OC}$=$\vec c$,用$\vec a$,$\vec b$,$\vec c$表示$\overrightarrow{MN}$,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}(\vec b+\vec c-\vec a)$ | B. | $\frac{1}{2}(\vec a+\vec b-\vec c)$) | C. | $\frac{1}{2}(\vec a-\vec b+\vec c)$ | D. | $\frac{1}{2}(\vec c-\vec a-\vec b)$ |
分析 根据所给的图形,在图形中看出要求的向量可以怎么得到,用减法把向量先变化成已知向量的差的形式,再利用向量的加法法则,得到结果.
解答 解:由题意知$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=$\frac{1}{2}$$\overrightarrow{OC}$-$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)
∵$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,
∴$\overrightarrow{MN}$=$\frac{1}{2}$($\overrightarrow{c}$-$\overrightarrow{b}$-$\overrightarrow{a}$)
故选:D.
点评 本题考查空间向量的加减法,本题解题的关键是在已知图形中尽量的应用几何体的已知棱表示要求的结果,本题是一个基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
9.有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
| A. | 264 | B. | 72 | C. | 266 | D. | 274 |
10.一程序框图如图所示,如果输出的函数值在区间[1,2]内,那么输入实数x的取值范围是( )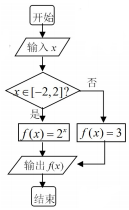

| A. | (-∞,0) | B. | [-1,0] | C. | [1,+∞) | D. | [0,1] |
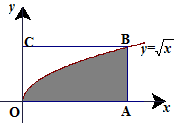 如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.
如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.