题目内容
15．已知命题p：?c＞0，使方程x2-x+c=0有解，则￢p为（ ）| A． | ?c＞0，方程x2-x+c=0无解 | B． | ?c≤0，方程x2-x+c=0有解 | ||
| C． | ?c＞0，使方程x2-x+c=0无解 | D． | ?c≤0，使方程x2-x+c=0有解 |
分析 直接利用特称命题的否定是全称命题写出结果即可．
解答 解：因为特称命题的否定是全称命题，命题p：?c＞0，使方程x2-x+c=0有解
则命题p的否定￢p是：?c＞0，方程x2-x+c=0无解．
故选：A．
点评 本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
已知全集U=R，集合A=$\left\{{x\left|{y=\sqrt{{x^2}-4x+3}}\right.}\right\}$，B={y|y=log2x，4＜x＜16}，
10．一程序框图如图所示，如果输出的函数值在区间[1，2]内，那么输入实数x的取值范围是（ ）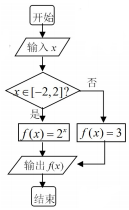
| A． | （-∞，0） | B． | [-1，0] | C． | [1，+∞） | D． | [0，1] |
20．下表是降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据，根据上表提供的数据，求出y关于x的线性回归方程y=0.75x+0.35，那么表中m=3.9．
| X | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
7．函数y=xex（e为自然对数的底）在（1，f（1））点处的切线方程是（ ）
| A． | y=2ex-e | B． | y=2ex-2e | C． | y=ex-e | D． | y=ex-1 |
4．设集合A={-2，-1，0，1，2}，B={x|x2+2x＜0}，则A∩（∁RB）=（ ）
| A． | {1，2} | B． | {0，1，2} | C． | {-2，1，2} | D． | {-2，0，1，2} |
5．已知命题“?x∈R，使4x2+（a-2）x+$\frac{1}{4}$≤0”是假命题，则实数a的取值范围是（ ）
| A． | （-∞，0） | B． | [0，4] | C． | [4，+∞） | D． | （0，4） |