题目内容
2.双曲线的中心在原点,离心率等于2,若它的一个顶点恰好是抛物线y2=8x的焦点,则双曲线的方程为$\frac{{x}^{2}}{1}-\frac{{y}^{2}}{3}=1$.分析 求出抛物线的焦点坐标,利用双曲线的离心率求出a,然后求解b,即可得到双曲线方程.
解答 解:双曲线的中心在原点,离心率等于2,若它的一个顶点恰好是抛物线y2=8x的焦点,
可得c=2,a=1,则b=$\sqrt{3}$,
所求的双曲线方程为:$\frac{{x}^{2}}{1}-\frac{{y}^{2}}{3}=1$.
故答案为:$\frac{{x}^{2}}{1}-\frac{{y}^{2}}{3}=1$.
点评 本题考查双曲线的简单性质的应用,双曲线方程的求法,考查计算能力.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
10.一程序框图如图所示,如果输出的函数值在区间[1,2]内,那么输入实数x的取值范围是( )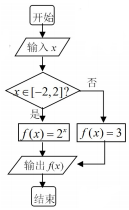

| A. | (-∞,0) | B. | [-1,0] | C. | [1,+∞) | D. | [0,1] |
7.函数y=xex(e为自然对数的底)在(1,f(1))点处的切线方程是( )
| A. | y=2ex-e | B. | y=2ex-2e | C. | y=ex-e | D. | y=ex-1 |
11.运行如图所示的算法框图,则输出的结果S为( )


| A. | $\frac{1}{2}$ | B. | 0 | C. | -1 | D. | $-\frac{3}{2}$ |
12.方程$(x+y-2)\sqrt{{x^2}+{y^2}-9}=0$表示的曲线是( )
| A. | 一条直线和一个圆 | B. | 一条直线和半个圆 | ||
| C. | 两条射线和一个圆 | D. | 一条线段和半个圆 |
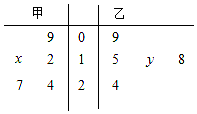 如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )
如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )