题目内容
已知：函数f(
)的定义域为[0，4]，则函数g（x）=f（x+2）的定义域为（ ）
| x |
| A、[0，2] | B、[-2，0] |
| C、[2，4] | D、R |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数f（
）的定义域，得到0≤x+2≤2，求出f（x+2）的定义域即可．
| x |
解答：
解：∵0≤x≤4，
∴0≤
≤2，
∴0≤x+2≤2，
∴-2≤x≤0，
故选：B．
∴0≤
| x |
∴0≤x+2≤2，
∴-2≤x≤0，
故选：B．
点评：本题考查了函数的定义域问题，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
下列说法不正确的是（ ）
A、“cosα=
| ||||
| B、命题P：?x∈R，使得x2+x-1＜0，则p：?x∈R，使得x2+x-1≥0 | ||||
| C、命题“在△ABC中，若A＞B，则sinA＞sinB”的逆否命题是真命题 | ||||
| D、若p∧q为假命题，则p∨q为假命题 |
在等比数列{an}中，若a1=2，a2+a5=0，{an}的n项和为Sn，则S2015+S2016=（ ）
| A、4032 | B、2 |
| C、-2 | D、-4030 |
| ∫ | 1 -1 |
| A、0 | B、2sin1 |
| C、2cos1 | D、2 |
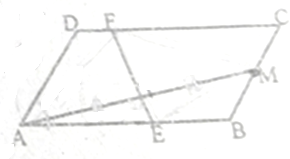已知，平行四边形ABCD中，AB=4，AD=2