Question

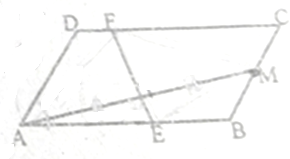已知，平行四边形ABCD中，AB=4，AD=2

2

，∠BAD=45°，M是BC中点，将平行四边形沿EF折叠，使A与M重合，求折痕EF的长度以及△AEM的面积．

Answer 1

考点：相似三角形的判定

专题：立体几何

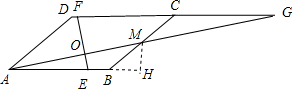
分析：若将平行四边形沿EF折叠，使A与M重合，则折痕EF是线段AM的垂直平分线，延长AM交DC的延长线与G点，过M作AB的垂线，垂足为H，利用三角形相似和勾股定理可求出OE的长度进而得到EF的长度，求出AE的长度后，代入三角形面积公式，可得△AEM的面积．

解答： 解：延长AM交DC的延长线与G点，过M作AB的垂线，垂足为H，
，
∵AB=4，AD=2

2

，∠BAD=45°，M是BC中点，
∴BM=

2

，BH=MH=1，
则AM=

(4+1)2+1

=

26

，
∵折痕EF是线段AM的垂直平分线，可得：
AO=

26

2

，△AOE∽△AHM，
∴OE=

MH

AH

•AO=

26

10

，
∵△AOE∽△COF且相似比为1：3，
故OF=3OE，则EF=4OE=

2 26

5

，
又由AE=

AO

AH

•AM=

13

5

，
故△AEM的面积S=

1

2

AE•MH=

13

10

点评：本题考查的知识点是三角形相似的判断与应用，三角形面积公式，难度中档．