题目内容
15.已知sin(α+β)=$\frac{1}{2}$,sin(α-β)=$\frac{1}{3}$,那么log5$\frac{tanα}{tanβ}$的值是1.分析 由两角和与差的正弦公式可得sinαcosβ和cosαsinβ的方程组,解方程组由同角三角函数基本关系可得$\frac{tanα}{tanβ}$,求对数可得.
解答 解:∵sin(α+β)=$\frac{1}{2}$,sin(α-β)=$\frac{1}{3}$,
∴sinαcosβ+cosαsinβ=$\frac{1}{2}$,sinαcosβ-cosαsinβ=$\frac{1}{3}$,
两式联立可解得sinαcosβ=$\frac{5}{12}$,cosαsinβ=$\frac{1}{12}$,
∴$\frac{tanα}{tanβ}$=$\frac{sinαcosβ}{cosαsinβ}$=5,
∴log5$\frac{tanα}{tanβ}$=log55=1
故答案为:1
点评 本题考查两角和与差的三角函数公式,涉及整体代入和对数的运算,属基础题.

练习册系列答案
相关题目
4.以(-2,1)为圆心且与直线x+y=3相切的圆的方程为( )
| A. | (x-2)2+(y+1)2=2 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=8 | D. | (x+2)2+(y-1)2=8 |
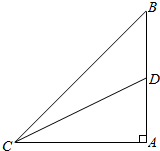 如图,AB是竖立在地面上的一根杆子,高为10m,D为AB的中点,在地面C处测得点B的仰角为45°,则在C处测点D的仰角应是多少(精确到0.1°)
如图,AB是竖立在地面上的一根杆子,高为10m,D为AB的中点,在地面C处测得点B的仰角为45°,则在C处测点D的仰角应是多少(精确到0.1°)
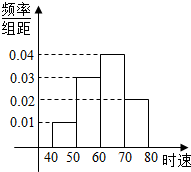 5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问:
5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问: