题目内容
12．
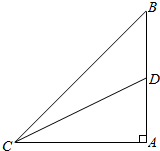如图，AB是竖立在地面上的一根杆子，高为10m，D为AB的中点，在地面C处测得点B的仰角为45°，则在C处测点D的仰角应是多少（精确到0.1°）
分析 AC=AB=10，则tan∠ACD=$\frac{1}{2}$．
解答 解：∵∠ACD=45°，∠A=90°，∴△ABC是等腰直角三角形，∴AC=AB=10，
∵D是AB的中点，∴AD=5，∴tan∠ACD=$\frac{AD}{AC}$=$\frac{1}{2}$．∴∠ACD≈26.6°．
∴在C处测点D的仰角约是26.6°．
点评 本题考查了解三角形的应用，属于基础题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
2．已知函数$f（x）=sin（x+\frac{π}{6}）cos（x+\frac{π}{6}）$，给出下列结论正确的是（ ）
| A． | f（x）的最小正周期是2π | B． | $f（x）的一条对称轴是x=\frac{π}{6}$ | ||
| C． | $f（x）的一个对称中心是（\frac{π}{6}，0）$ | D． | $f（x-\frac{π}{6}）是奇函数$ |
1．已知${A}_{n+1}^{2}$-${A}_{n}^{2}$=10，则n的值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |