题目内容
10.求f(x)=$\frac{{k}^{2}}{x}$+x,k>0的极值.分析 先求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:∵f(x)=$\frac{{k}^{2}}{x}$+x,k>0,
∴f′(x)=1-$\frac{{k}^{2}}{{x}^{2}}$=$\frac{{x}^{2}{-k}^{2}}{{x}^{2}}$,
令f′(x)>0,解得x>k或x<-k,
令f′(x)<0,解得:0<x<k或-k<x<0,
∴f(x)在(-∞,-k),(k,+∞)递增,在(-k,0),(0,k)递减,
∴f(x)极小值=f(k)=2k,f(x)极大值=f(-k)=-2k.
点评 本题考查了求函数的单调性、极值问题,考查导数的应用,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知下列问题:
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.已知α是第二象限角,其终边上一点$P(x,\sqrt{3})$,且$cosα=\frac{{\sqrt{2}}}{4}x$,则sinα=( )
| A. | $-\frac{{\sqrt{6}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
20.数列{2n-11}的前n项和Sn中最小的是( )
| A. | S4 | B. | S5 | C. | S6 | D. | S7 |
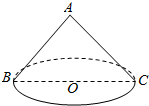 如图,已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形.试求:
如图,已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形.试求: