题目内容
7.已知对任意n∈N*,点$({a_{n+1}}^2-\frac{1}{2}{n^2},{a_n}(2{a_{n+1}}-{a_n})+\frac{1}{2}{n^2})$,在直线y=x上,若a1=1,an>0,则an=$\frac{{{n^2}-n+2}}{2}$.分析 由已知可得${a}_{n}(2{a}_{n+1}-{a}_{n})+\frac{1}{2}{n}^{2}={{a}_{n+1}}^{2}-\frac{1}{2}{n}^{2}$,整理得$({a}_{n+1}-{a}_{n})^{2}={n}^{2}$,结合an>0,可得an+1-an=n,然后利用累加法求得答案.
解答 解:∵点$({a_{n+1}}^2-\frac{1}{2}{n^2},{a_n}(2{a_{n+1}}-{a_n})+\frac{1}{2}{n^2})$在直线y=x上,
∴${a}_{n}(2{a}_{n+1}-{a}_{n})+\frac{1}{2}{n}^{2}={{a}_{n+1}}^{2}-\frac{1}{2}{n}^{2}$,
即${{a}_{n+1}}^{2}-2{a}_{n+1}{a}_{n}+{{a}_{n}}^{2}={n}^{2}$,
∴$({a}_{n+1}-{a}_{n})^{2}={n}^{2}$,
则an+1-an=±n,
∵an>0,
∴an+1-an=n,
则an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(n-1)+(n-2)+…+1+1=$\frac{n(n-1)}{2}+1=\frac{{n}^{2}-n+2}{2}$;
故答案为:$\frac{{{n^2}-n+2}}{2}$.
点评 本题考查数列递推式,考查了数列的函数特性,训练了累加法求数列的通项公式,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知α是第二象限角,其终边上一点$P(x,\sqrt{3})$,且$cosα=\frac{{\sqrt{2}}}{4}x$,则sinα=( )
| A. | $-\frac{{\sqrt{6}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
12.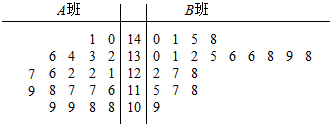 为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
市数学会规定:140分以上(含140分)为市级一等奖,135分以上(含135分)为市级二等奖,100分以上(含100分)为市级三等奖.
(1)由茎叶图判断A班和B班的平均分$\overline{{x}_{A}}$,$\overline{{x}_{B}}$的大小(只需写出结论);
(2)按照规则:获得市一等奖、二等奖的同学才能获得省里组织的“全国数学联赛”复赛资格,我们称这些同学为“种子选手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为称为“种子选手”与班级有关?
(3)若在“种子选手”中选出3人,其中含有“获市级一等奖”的同学中为X人,求X的分布列及数学期望.
下面临界值表仅供参考:
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:市数学会规定:140分以上(含140分)为市级一等奖,135分以上(含135分)为市级二等奖,100分以上(含100分)为市级三等奖.
(1)由茎叶图判断A班和B班的平均分$\overline{{x}_{A}}$,$\overline{{x}_{B}}$的大小(只需写出结论);
(2)按照规则:获得市一等奖、二等奖的同学才能获得省里组织的“全国数学联赛”复赛资格,我们称这些同学为“种子选手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为称为“种子选手”与班级有关?
| A班 | B班 | 合计 | |
| 种子选手 | |||
| 非种子选手 | |||
| 合计 |
下面临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
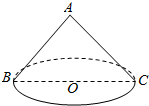 如图,已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形.试求:
如图,已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形.试求: