题目内容

下列命题正确的是（　　）
A、函数y=cos（x+
π
3
）的图象是关于点（（
π
6
，0）成中心对称的图形
B、函数y=cos4x-sin4x的最小正周期为2π
C、函数y=sin（2x+
π
3
）在区间（-
π
3
，
π
6
）内单调递增
D、函数y=tan（x+
π
3
）的图象是关于直线x=
π
6
成轴对称的图形
考点：命题的真假判断与应用
专题：简易逻辑
分析：A．利用f(
π
6
)=cos(
π
6
+
π
3
)=cos
π
2
=0，可得函数f（x）的图象是关于点（
π
6
，0）成中心对称的图形；
B．利用倍角公式可得：函数y=cos2x的最小正周期为
2π
2
=π；
C．由x∈（-
π
3
，
π
6
），可得-
π
3
＜2x+
π
3
＜
2π
3
，因此函数y=sin（2x+
π
3
）在区间（-
π
3
，
π
6
）内不单调，不正确；
D．函数y=tan（x+
π
3
）的图象是关于直线x=
π
6
不成轴对称的图形，而(
π
6
，0)是它的一个对称中心．
解答： 解：对于A．∵f（x）=cos（x+
π
3
），∴f(
π
6
)=cos(
π
6
+
π
3
)=cos
π
2
=0，因此函数f（x）的图象是关于点（
π
6
，0）成中心对称的图形，正确；
对于B．函数y=cos4x-sin4x=cos2x-sin2x=cos2x的最小正周期为
2π
2
=π，因此不正确；
对于C．∵x∈（-
π
3
，
π
6
），∴-
π
3
＜2x+
π
3
＜
2π
3
，∴函数y=sin（2x+
π
3
）在区间（-
π
3
，
π
6
）内不单调，不正确；
对于D．函数y=tan（x+
π
3
）的图象是关于直线x=
π
6
不成轴对称的图形，而(
π
6
，0)是它的一个对称中心，不正确．
故选：A．
点评：本题考查了三角函数的图象与性质、简易逻辑的判定，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
若将函数f（x）=x5表示为f（x）=a0+a1（x-1）+a2（x-1）2+a3（x-1）3+a4（x-1）4+a5（x-1）5，其中a0，a1，a2，…a5为实数，则a1+a2+a3+a4+a5=
 
．
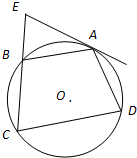如图，四边形ABCD的外接圆为⊙O，EA是⊙O的切线，CB的延长线与EA相交于点E，AB=AD．求证：AB2=BE•CD．
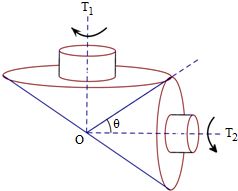在△ABC中，满足AB⊥AC，AB=AC=2．若一个椭圆恰好以C为一个焦点，另一个焦点在线段AB上，且A，B均在此椭圆上，则该椭圆的离心率为
 
．
如图所示，某传动装置由两个陀螺T1，T2组成，陀螺之间没有滑动．每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成，每个圆柱的底面半径和高都是相应圆锥底面半径的
1
3
，且T1，T2的轴相互垂直，它们相接触的直线与T2的轴所成角θ=arctan
2
3
．若陀螺T2中圆锥的底面半径为r（r＞0）．
（1）求陀螺T2的体积；
（2）当陀螺T2转动一圈时，陀螺T1中圆锥底面圆周上一点P转动到点P1，求P与P1之间的距离．
设函数f（x）=sinxcosx-
3
cos（π+x）cosx（x∈R）．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函数y=f（x0的图象按b=（
π
4
，
3
2
）平移后得到函数y=g（x）的图象，求y=g（x）在（0，
π
4
]上的最大值．
设t为实数，|
e1
|=2，|
e2
|=1，
e1
，
e2
的夹角为
π
3
，若向量2t
e1
+7
e2
与向量
e1
+t
e2
的夹角为钝角，则实数t的取值范围是
 
．
已知函数f（x）=x2+2|x|-8，定义域为[a，b]（a，b∈Z），值域为[-8，0]，则满足条件的整数对（a，b）有
 
对．
若A为抛物线y=
1
4
x2的顶点，过抛物线焦点的直线交抛物线于B、C两点，则
AB
•
AC
等于（　　）
A、-3B、3C、5D、-5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网