题目内容
若将函数f(x)=x5表示为f(x)=a0+a1(x-1)+a2(x-1)2+a3(x-1)3+a4(x-1)4+a5(x-1)5,其中a0,a1,a2,…a5为实数,则a1+a2+a3+a4+a5= .
考点:二项式系数的性质
专题:二项式定理
分析:在所给的等式中,令x=1可得a0=1.再令x=2可得1+a1+a2+a3+a4+a5=32,从而求得a1+a2+a3+a4+a5的值.
解答:
解:由于f(x)=a0+a1(x-1)+a2(x-1)2+a3(x-1)3+a4(x-1)4+a5(x-1)5 =[1+(x-1)]5,
令x=1可得a0=1.
再令x=2可得1+a1+a2+a3+a4+a5=32,∴a1+a2+a3+a4+a5=31,
故答案为:31.
令x=1可得a0=1.
再令x=2可得1+a1+a2+a3+a4+a5=32,∴a1+a2+a3+a4+a5=31,
故答案为:31.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
相关题目
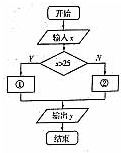 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )| A、y=0.8x y=0.5x |
| B、y=0.5x y=0.8x |
| C、y=25×0.5+(x-25)×0.8 y=0.5x |
| D、y=25×0.5+0.8x y=0.8x |
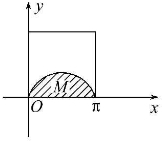 如图,在边长为π的正方形内的正弦曲线y=sinx与x轴围成的区域记为M(图中阴影部分),随机往正方形内投一个点P,则点P落在区域M内的概率是( )
如图,在边长为π的正方形内的正弦曲线y=sinx与x轴围成的区域记为M(图中阴影部分),随机往正方形内投一个点P,则点P落在区域M内的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在边长为a的正方形内随机取一个点,则此点落在该正方形的内切圆内部的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合M={x|x<2012},N={x|0<x≤2012},则M∪N=( )
| A、M |
| B、N |
| C、{x|x≤2012} |
| D、{x|0<x<2012} |
下列命题正确的是( )
A、函数y=cos(x+
| ||||||
| B、函数y=cos4x-sin4x的最小正周期为2π | ||||||
C、函数y=sin(2x+
| ||||||
D、函数y=tan(x+
|