题目内容
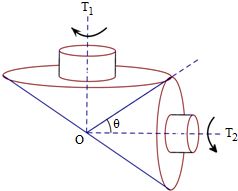 如图所示,某传动装置由两个陀螺T1,T2组成,陀螺之间没有滑动.每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的
如图所示,某传动装置由两个陀螺T1,T2组成,陀螺之间没有滑动.每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的| 1 |
| 3 |
| 2 |
| 3 |
(1)求陀螺T2的体积;
(2)当陀螺T2转动一圈时,陀螺T1中圆锥底面圆周上一点P转动到点P1,求P与P1之间的距离.
考点:旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)设陀螺T2圆锥的高为h,可得h=
r,进而可得陀螺T2圆柱的底面半径和高为
,进而求出陀螺T2的体积;
(2)设陀螺T1圆锥底面圆心为O,可得
=2πr,进而利用弧长公式,求出圆心角,进而可得P与P1之间的距离.
| 3 |
| 2 |
| r |
| 3 |
(2)设陀螺T1圆锥底面圆心为O,可得
 |
| PP1 |
解答:
解:(1)设陀螺T2圆锥的高为h,
则
=
,
即h=
r’
得陀螺T2圆柱的底面半径和高为
,
V柱=π(
)2
=
πr3
V椎=
πr2•
r=
πr3
VT2=V柱+V椎=
πr3
(2)设陀螺T1圆锥底面圆心为O,

则
=2πr,
得∠POP1=
=
=
在△POP1中,PP1=
OP=
r
则
| r |
| h |
| 2 |
| 3 |
即h=
| 3 |
| 2 |
得陀螺T2圆柱的底面半径和高为
| r |
| 3 |
V柱=π(
| r |
| 3 |
| r |
| 3 |
| 1 |
| 27 |
V椎=
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
VT2=V柱+V椎=
| 29 |
| 54 |
(2)设陀螺T1圆锥底面圆心为O,

则
 |
| PP1 |
得∠POP1=
| ||
| OP |
| 2πr | ||
|
| 4π |
| 3 |
在△POP1中,PP1=
| 3 |
3
| ||
| 2 |
点评:本题考查的知识点是旋转体的体积公式,弧长公式,是三角函数与空间几何的综合应用,难度中档.

练习册系列答案
相关题目
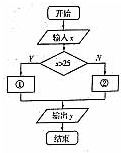 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )| A、y=0.8x y=0.5x |
| B、y=0.5x y=0.8x |
| C、y=25×0.5+(x-25)×0.8 y=0.5x |
| D、y=25×0.5+0.8x y=0.8x |
已知数列{an}的前n项和为Sn,且Sn=2an-1(n∈N*),则a4=( )
| A、8 | B、16 | C、31 | D、32 |
下列命题正确的是( )
A、函数y=cos(x+
| ||||||
| B、函数y=cos4x-sin4x的最小正周期为2π | ||||||
C、函数y=sin(2x+
| ||||||
D、函数y=tan(x+
|
设是虚数单位,若复数
为实数,则实数a的值为( )
| a-i |
| 2+i |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
在等比数列{an}中,a1=1,a4=8,那么{an}的前5项和是( )
| A、-31 | B、15 | C、31 | D、63 |