题目内容
7.sin21°+sin22°+sin23°+…+sin288°+sin289°的值为 ( )| A. | 89 | B. | 44 | C. | $44\frac{1}{2}$ | D. | $44+\frac{{\sqrt{2}}}{2}$ |
分析 通过诱导公式sin89°=cos1°,得出sin21°+cos21°=1,依此类推,得出原式=44×1+sin245°,得出答案.
解答 解:∵sin89°=sin(90°-1°)=cos1°,
∴sin21°+sin289°=sin21°+cos21°=1,
同理sin2°+sin88°=1,…sin44°+sin46°=1,
∴sin21°+sin22°+sin23°+…+sin288°+sin289°=44+$\frac{1}{2}$=44$\frac{1}{2}$.
故选:C.
点评 分析本题主要考查了三角函数中的诱导公式的运用.属基础题.

练习册系列答案
相关题目
2.△ABC中,已知a=7,b=14,A=30°,则△ABC有( )
| A. | 一解 | B. | 二解 | C. | 无解 | D. | 一解或二解 |
19.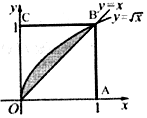 向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
 向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
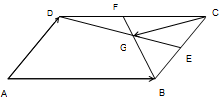 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量