题目内容
18.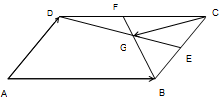 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量(1)$\overrightarrow{DB}$
(2)$\overrightarrow{AC}$
(3)$\overrightarrow{DE}$
(4)$\overrightarrow{CG}$.
分析 (1)根据向量减法的几何意义表示;
(2)根据向量加法的平行四边形法则表示;
(3)根据向量加法和数乘的几何意义表示;
(4)根据A,B,C三点共线时,$\overrightarrow{OB}=x\overrightarrow{OA}+y\overrightarrow{OC}$且x+y=1来表示.
解答 解:(1)$\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{a}-\overrightarrow{b}$;
(2)$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{a}+\overrightarrow{b}$;
(3)$\overrightarrow{DE}=\overrightarrow{DC}+\overrightarrow{CE}$
=$\overrightarrow{DC}+\frac{1}{2}\overrightarrow{CB}$
=$\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$
=$\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$;
(4)设$\overrightarrow{CG}=m\overrightarrow{CD}+n\overrightarrow{CE}$,则:
$\overrightarrow{CG}=2m\overrightarrow{CF}+\frac{n}{2}\overrightarrow{CB}$;
∴$\left\{\begin{array}{l}{m+n=1}\\{2m+\frac{n}{2}=1}\end{array}\right.$;
解得$m=\frac{1}{3},n=\frac{2}{3}$;
∴$\overrightarrow{CG}=\frac{1}{3}\overrightarrow{CD}+\frac{2}{3}\overrightarrow{CE}$
=$\frac{1}{3}\overrightarrow{CD}+\frac{1}{3}\overrightarrow{CB}$
=$-\frac{1}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}$
=$-\frac{1}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}$.
点评 考查向量加法、减法及数乘的几何意义,向量加法的平行四边形法则,以及三点A,B,C共线的充要条件:$\overrightarrow{OB}=x\overrightarrow{OA}+y\overrightarrow{OC}$且x+y=1.

 阅读快车系列答案
阅读快车系列答案| A. | [-$\frac{1}{2}$,1] | B. | [-1,$\frac{1}{2}$] | C. | [-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{5π}{6}$ | D. | π |
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
| A. | 89 | B. | 44 | C. | $44\frac{1}{2}$ | D. | $44+\frac{{\sqrt{2}}}{2}$ |