题目内容
19．
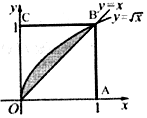向如图所示的正方形OABC内任意投一点，该点恰好落在图中阴影部分的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
分析 根据几何概型概率公式，分别求出正方形面积和阴影部分的面积，利用面积比解得．
解答 解：由题意，本题是几何概型的概率问题，正方形的面积为1，
阴影部分的面积为${∫}_{0}^{1}$（$\sqrt{x}$-x）dx=（$\frac{2}{3}{x}^{\frac{3}{2}}$-$\frac{1}{2}$x2）|${\;}_{0}^{1}$=$\frac{2}{3}-\frac{1}{2}$=$\frac{1}{6}$，
由几何概型的概率公式得，
点落在阴影部分的概率为P=$\frac{1}{6}$．
故选D．
点评 本题考查了几何概型的计算问题，涉及定积分在求面积中的应用，关键是正确算出阴影部分的面积，是基础题目．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
9．定义min{a，b}=$\left\{\begin{array}{l}{a，（a≤b）}\\{b，（a＞b）}\end{array}\right.$，若函数f（x）=min{sin（2x+$\frac{π}{6}$），cos2x}，且f（x）在区间[s，t]上的值域为[-1，$\frac{1}{2}$]，则区间[s．t]长度的最大值为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{2}$ | C． | $\frac{5π}{6}$ | D． | π |
10．已知$sin（\frac{2π}{3}+α）=\frac{1}{3}$，则$cos（\frac{5π}{6}-α）$=（ ）
| A． | $-\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $-\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
7．sin21°+sin22°+sin23°+…+sin288°+sin289°的值为 （ ）
| A． | 89 | B． | 44 | C． | $44\frac{1}{2}$ | D． | $44+\frac{{\sqrt{2}}}{2}$ |