题目内容
12.若函数f(x)在x=a处的导数为A,则$\lim_{△x→0}\frac{f(a+4△x)-f(a+5△x)}{△x}$=( )| A. | -A | B. | A | C. | 2A | D. | -2A |
分析 化简$\underset{lim}{△x→0}$$\frac{f(a+4△x)-f(a)}{△x}$+$\underset{lim}{△x→0}$$\frac{f(a)-f(a+5△x)}{△x}$,根据导数的定义,即可求得答案.
解答 解:$\lim_{△x→0}\frac{f(a+4△x)-f(a+5△x)}{△x}$=$\underset{lim}{△x→0}$$\frac{f(a+4△x)-f(a)+f(a)-f(a+5△x)}{△x}$,
=$\underset{lim}{△x→0}$$\frac{f(a+4△x)-f(a)}{△x}$+$\underset{lim}{△x→0}$$\frac{f(a)-f(a+5△x)}{△x}$,
=4$\underset{lim}{△x→0}$$\frac{f(a+4△x)-f(a)}{4△x}$-5$\underset{lim}{△x→0}$$\frac{f(a+5△x)-f(a)}{5△x}$,
=4f′(a)-5f′(a)
=-A,
$\lim_{△x→0}\frac{f(a+4△x)-f(a+5△x)}{△x}$=-A,
故选A.
点评 本题考查极限及运算,考查导数的定义,考查计算能力,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
2.a,b,c是△ABC中角A,B,C的对边,则直线sinAx+ay+c=0与sinBx+by=0的位置关系是( )
| A. | 相交 | B. | 重合 | C. | 垂直 | D. | 平行 |
7.sin21°+sin22°+sin23°+…+sin288°+sin289°的值为 ( )
| A. | 89 | B. | 44 | C. | $44\frac{1}{2}$ | D. | $44+\frac{{\sqrt{2}}}{2}$ |

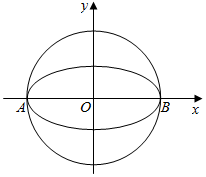 如图,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,其左顶点A在圆O:x2+y2=16上.