题目内容
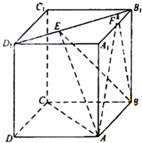 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有①AC⊥面BEF;
②AF与BE相交;
③若P为AA1上的一动点,则三棱锥P-BEF的体积为定值;
④在空间与直线DD1,AC,B1C1都相交的直线只有1条.
考点:空间中直线与直线之间的位置关系
专题:计算题,空间位置关系与距离
分析:连接BD,交AC于O,由线面垂直的性质定理和判定定理,即可判断①;
由两异面直线的判定方法,即可得到AF与BE为异面直线,进而判断②;
运用棱锥的体积公式,由于EF=1,矩形BDD1B1内B到EF的距离为1,则三角形BEF的面积为
,再由P在棱AA1上,P到平面BEF的距离,即为A到平面BDD1B1的距离,即可得到体积,从而判断③;
由于平面BDD1B1与直线DD1,AC,B1C1都有交点,则所求直线在平面BDD1B1,由于平面BDD1B1与直线AC交于O,与直线C1B1交于B1,即可判断④.
由两异面直线的判定方法,即可得到AF与BE为异面直线,进而判断②;
运用棱锥的体积公式,由于EF=1,矩形BDD1B1内B到EF的距离为1,则三角形BEF的面积为
| 1 |
| 2 |
由于平面BDD1B1与直线DD1,AC,B1C1都有交点,则所求直线在平面BDD1B1,由于平面BDD1B1与直线AC交于O,与直线C1B1交于B1,即可判断④.
解答:
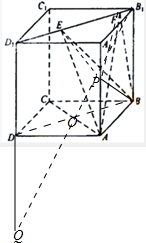 解:对于①,连接BD,交AC于O,则AC⊥BD,又BB1⊥平面ABCD,则AC⊥BB1,
解:对于①,连接BD,交AC于O,则AC⊥BD,又BB1⊥平面ABCD,则AC⊥BB1,
则有AC⊥平面BDD1B1,即AC⊥面BEF,故①对;
对于②,由于BE是平面BDD1B1内一直线,F不在直线BE上,且F在平面BDD1B1内,
点A不在平面BDD1B1内,由异面直线的判定可得,AF与BE为异面直线,故②错;
对于③,三棱锥P-BEF的体积为
S△BEF•h,由于EF=1,矩形BDD1B1内B到EF的距离为1,则三角形BEF的面积为
,由于P在棱AA1上,P到平面BEF的距离,即为A到平面BDD1B1的距离,由于AC⊥平面BDD1B1,则h=AO=
,则三棱锥P-BEF的体积为
,故③对;
对于④,由于平面BDD1B1与直线DD1,AC,B1C1都有交点,
则所求直线在平面BDD1B1,由于平面BDD1B1与直线AC交于O,与直线C1B1交于B1,
连接OB1,延长与D1D延长交于Q,即为所求直线,故④对.
故答案为:①③④
 解:对于①,连接BD,交AC于O,则AC⊥BD,又BB1⊥平面ABCD,则AC⊥BB1,
解:对于①,连接BD,交AC于O,则AC⊥BD,又BB1⊥平面ABCD,则AC⊥BB1,则有AC⊥平面BDD1B1,即AC⊥面BEF,故①对;
对于②,由于BE是平面BDD1B1内一直线,F不在直线BE上,且F在平面BDD1B1内,
点A不在平面BDD1B1内,由异面直线的判定可得,AF与BE为异面直线,故②错;
对于③,三棱锥P-BEF的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
对于④,由于平面BDD1B1与直线DD1,AC,B1C1都有交点,
则所求直线在平面BDD1B1,由于平面BDD1B1与直线AC交于O,与直线C1B1交于B1,
连接OB1,延长与D1D延长交于Q,即为所求直线,故④对.
故答案为:①③④
点评:本题考查空间直线与平面的位置关系,考查线面垂直的判定和性质,两直线的位置关系,考查三棱锥体积的求法,考查运算能力和推理能力,属于中档题和易错题.

练习册系列答案
相关题目
在△ABC中,若(a+c)(a-c)=b(b-c),则∠A=( )
| A、90° | B、60° |
| C、120° | D、150° |
α,β是两个不重合的平面,在下列条件中,可判定α∥β的是( )
| A、α,β都与平面γ垂直 |
| B、α内不共线的三点到β的距离相等 |
| C、l,m是α内的两条直线且l∥β,m∥β |
| D、l,m是两条异面直线且l∥α,m∥α,l∥β,m∥β |
若a=20.6,b=log22,c=ln0.6,则( )
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |