题目内容
α，β是两个不重合的平面，在下列条件中，可判定α∥β的是（ ）
| A、α，β都与平面γ垂直 |
| B、α内不共线的三点到β的距离相等 |
| C、l，m是α内的两条直线且l∥β，m∥β |
| D、l，m是两条异面直线且l∥α，m∥α，l∥β，m∥β |
考点：平面与平面之间的位置关系
专题：空间位置关系与距离,空间角
分析：通过举例子，和特殊图形来进行判断，或使用排除法．
解答：
解：利用排除法：对于A：如图所示
对于B：α内不共线的三点到β的距离相等，必须是α内不共线的三点在β的同侧．
对于C：l，m是α内的两条直线且l∥β，m∥β，l和m不是平行直线．
故选：D
解：利用排除法：对于A：如图所示对于B：α内不共线的三点到β的距离相等，必须是α内不共线的三点在β的同侧．
对于C：l，m是α内的两条直线且l∥β，m∥β，l和m不是平行直线．
故选：D
点评：本题考查的知识要点：立体几何中的定义和判定定理的应用．特殊图形和特殊值是解决此问题的关键．
练习册系列答案
相关题目
已知角α的终边经过点（3，-4），则tan
=（ ）
| α |
| 2 |
A、-
| ||
B、-
| ||
| C、2 | ||
| D、3 |
设0＜a＜1，m=loga(a2+1)，n=loga（a+1），p=logaa，则m，n，p的大小关系是（ ）
| A、n＞m＞p |
| B、m＞p＞n |
| C、m＞n＞p |
| D、p＞m＞n |
设集合U={1，2，3，4，5}，A={1，2，3}，B={2，5}，则（∁UA）∩（∁UB）=（ ）
| A、{2} | B、{2，3} |
| C、{4} | D、{1，3} |
如果(4x2-
)n的展开式中含有非零常数项，则正整数n的最小值为（ ）
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
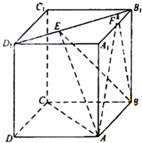如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=1，则下列结论中正确的有