题目内容
已知命题p：0不是偶数，命题q：函数f（x）=log2x的图象与函数f（x）=x2-4x+3的图象有两个交点，试写出命题“p∨q”“p∧q”“￢p”，并判断真假．
考点：复合命题的真假
专题：常规题型,简易逻辑
分析：由题意，命题p是假命题，命题q是真命题，写出“p∨q”（用或联结），“p∧q”（用且联结），“￢p”（否定），判断真假即可．
解答：
解：命题p是假命题，命题q是真命题；
∴p∨q：0不是偶数或函数f（x）=log2x的图象与函数f（x）=x2-4x+3的图象有两个交点，真；
p∧q：0不是偶数且函数f（x）=log2x的图象与函数f（x）=x2-4x+3的图象有两个交点，假；
￢p：0是偶数，真．
∴p∨q：0不是偶数或函数f（x）=log2x的图象与函数f（x）=x2-4x+3的图象有两个交点，真；
p∧q：0不是偶数且函数f（x）=log2x的图象与函数f（x）=x2-4x+3的图象有两个交点，假；
￢p：0是偶数，真．
点评：本题考查了复合命题的写法与真假性的判断，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知集合A={2，3，4，5}，B={3，5，6}，则A∩B=（ ）
| A、{3} |
| B、{2，4} |
| C、{2，3，4，5，6} |
| D、{3，5} |
设集合U={1，2，3，4，5}，A={1，2，3}，B={2，5}，则（∁UA）∩（∁UB）=（ ）
| A、{2} | B、{2，3} |
| C、{4} | D、{1，3} |
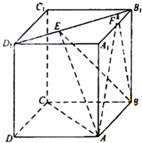如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=1，则下列结论中正确的有实数x、y满足不等式组
，且z=ax+y（a＞0）取最小值的最优解有无穷多个，则实数a的取值是（ ）
|
A、-
| ||
| B、1 | ||
| C、2 | ||
| D、无法确定 |