题目内容
已知数列{an}是等差数列,且a2+a5=19,a3+a6=25.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an-bn}是首项为2,公比为2的等比数列,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an-bn}是首项为2,公比为2的等比数列,求数列{bn}的前n项和Sn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(I)利用等差数列的通项公式即可得出;
(II)利用等比数列的通项公式、等差数列与等比数列的前n项和公式即可得出.
(II)利用等比数列的通项公式、等差数列与等比数列的前n项和公式即可得出.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,
∵a2+a5=19,a3+a6=25.
∴
,
解得
.
∴an=3n-1.
(Ⅱ)∵数列{an-bn}是首项为2,公比为2的等比数列,
∴an-bn=2n,
∴bn=3n-1-2n.
∴数列{bn}的前n项和Sn=
-
=
-2n+1.
∵a2+a5=19,a3+a6=25.
∴
|
解得
|
∴an=3n-1.
(Ⅱ)∵数列{an-bn}是首项为2,公比为2的等比数列,
∴an-bn=2n,
∴bn=3n-1-2n.
∴数列{bn}的前n项和Sn=
| n(3n+1) |
| 2 |
| 2(2n-1) |
| 2-1 |
| 3n2+n+4 |
| 2 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式,属于基础题.

练习册系列答案
相关题目
设集合P={0,1},那么集合P的子集个数是( )
| A、1 | B、2 | C、3 | D、4 |
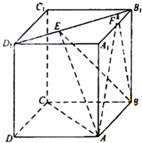 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有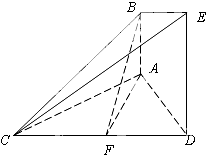 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 设地球半径为R,北纬30°圈上有A,B两地,它们的经度相差120°,则这两地间的纬度线的长为
设地球半径为R,北纬30°圈上有A,B两地,它们的经度相差120°,则这两地间的纬度线的长为