题目内容
已知二次函数f(x)=ax2+bx+c(其中a≠0)满足下列3个条件:
①f(x)的图象过坐标原点;
②对于任意x∈R都有f(-
+x)=f(-
-x)成立;
③方程f(x)=x有两个相等的实数根,令g(x)=f(x)-|λx-1|(其中λ>0),
(1)求函数f(x)的表达式;
(2)求函数g(x)的单调区间(直接写出结果即可);
(3)研究函数g(x)在区间(0,1)上的零点个数.
①f(x)的图象过坐标原点;
②对于任意x∈R都有f(-
| 1 |
| 2 |
| 1 |
| 2 |
③方程f(x)=x有两个相等的实数根,令g(x)=f(x)-|λx-1|(其中λ>0),
(1)求函数f(x)的表达式;
(2)求函数g(x)的单调区间(直接写出结果即可);
(3)研究函数g(x)在区间(0,1)上的零点个数.
考点:函数与方程的综合运用,带绝对值的函数,函数单调性的判断与证明,二次函数的性质,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)利用f(0)=0求出c.通过函数的对称轴,得到a=b,通过方程f(x)=x有两个相等的实数根,即可求函数f(x)的表达式;
(2)化简函数g(x)的表达式为分段函数,通过x≥
时,结合函数g(x)=x2+(1-λ)x+1的对称轴为求出单调求解,当x<
时类似求解函数单调区间.
(3)结合(2)的函数的单调性,即可研究函数g(x)在区间(0,1)上的零点个数.
(2)化简函数g(x)的表达式为分段函数,通过x≥
| 1 |
| λ |
| 1 |
| λ |
(3)结合(2)的函数的单调性,即可研究函数g(x)在区间(0,1)上的零点个数.
解答:
解:(1)由题意得f(0)=0,即c=0.…(1分)
∵对于任意x∈R都有f(-
+x)=f(-
-x),
∴对称轴为x=-
,即-
=-
,即a=b.
∴f(x)=ax2+ax,
∵方程f(x)=x仅有一根,即方程ax2+(a-1)x=0仅有一根,
∴△=0,即(a-1)2=0,即a=1.
∴f(x)=x2+x. …(4分)
(2)g(x)=f(x)-|λx-1|=
①当x≥
时,函数g(x)=x2+(1-λ)x+1的对称轴为x=
,
若
≤
,即0<λ≤2,函数g(x)在(
,+∞)上单调递增;
若
>
,即λ>2,函数g(x)在(
,+∞)上单调递增,在(
,
)上递减.
②当x<
时,函数g(x)=x2+(1+λ)x-1的对称轴为x=-
<
,
则函数g(x)在(-
,
)上单调递增,在(-∞,-
)上单调递减.
综上所述,
当0<λ≤2时,函数g(x)增区间为(-
,+∞),减区间为(-∞,-
);
当λ>2时,函数g(x)增区间为(-
,
)、(
,+∞),减区间为(-∞,-
)、(
,
). …(9分)
(3)①当0<λ≤2时,由(2)知函数g(x)在区间(0,1)上单调递增,
又g(0)=-1<0,g(1)=2-|λ-1|>0,
故函数g(x)在区间(0,1)上只有一个零点. …(12分)
②当λ>2时,则
<
<1,而g(0)=-1<0,g(
)=
+
>0,g(1)=2-|λ-1|,
(ⅰ)若2<λ≤3,由于
<
≤1,
且g(
)=(
)2+(1-λ)•
+1=-
+1≥0,
此时,函数g(x)在区间(0,1)上只有一个零点;
(ⅱ)若λ>3,由于
>1且g(1)=2-|λ-1|<0,此时g(x)在区间(0,1)
上有两个不同的零点.
综上所述,
当0<λ≤3时,函数g(x)在区间(0,1)上只有一个零点;
当λ>3时,函数g(x)在区间(0,1)上有两个不同的零点. …(16分)
∵对于任意x∈R都有f(-
| 1 |
| 2 |
| 1 |
| 2 |
∴对称轴为x=-
| 1 |
| 2 |
| b |
| 2a |
| 1 |
| 2 |
∴f(x)=ax2+ax,
∵方程f(x)=x仅有一根,即方程ax2+(a-1)x=0仅有一根,
∴△=0,即(a-1)2=0,即a=1.
∴f(x)=x2+x. …(4分)
(2)g(x)=f(x)-|λx-1|=
|
①当x≥
| 1 |
| λ |
| λ-1 |
| 2 |
若
| λ-1 |
| 2 |
| 1 |
| λ |
| 1 |
| λ |
若
| λ-1 |
| 2 |
| 1 |
| λ |
| λ-1 |
| 2 |
| 1 |
| λ |
| λ-1 |
| 2 |
②当x<
| 1 |
| λ |
| 1+λ |
| 2 |
| 1 |
| λ |
则函数g(x)在(-
| 1+λ |
| 2 |
| 1 |
| λ |
| 1+λ |
| 2 |
综上所述,
当0<λ≤2时,函数g(x)增区间为(-
| 1+λ |
| 2 |
| 1+λ |
| 2 |
当λ>2时,函数g(x)增区间为(-
| 1+λ |
| 2 |
| 1 |
| λ |
| λ-1 |
| 2 |
| 1+λ |
| 2 |
| 1 |
| λ |
| λ-1 |
| 2 |
(3)①当0<λ≤2时,由(2)知函数g(x)在区间(0,1)上单调递增,
又g(0)=-1<0,g(1)=2-|λ-1|>0,
故函数g(x)在区间(0,1)上只有一个零点. …(12分)
②当λ>2时,则
| 1 |
| λ |
| 1 |
| 2 |
| 1 |
| λ |
| 1 |
| λ2 |
| 1 |
| λ |
(ⅰ)若2<λ≤3,由于
| 1 |
| λ |
| λ-1 |
| 2 |
且g(
| λ-1 |
| 2 |
| λ-1 |
| 2 |
| λ-1 |
| 2 |
| (λ-1)2 |
| 4 |
此时,函数g(x)在区间(0,1)上只有一个零点;
(ⅱ)若λ>3,由于
| λ-1 |
| 2 |
上有两个不同的零点.
综上所述,
当0<λ≤3时,函数g(x)在区间(0,1)上只有一个零点;
当λ>3时,函数g(x)在区间(0,1)上有两个不同的零点. …(16分)
点评:本题考查函数的单调性的应用,分类讨论思想的应用,考查函数的零点解析式的求法,二次函数的性质的应用,是中档题.

练习册系列答案
相关题目
等差数列{an}的前3项和为30,前6项和为100,则它的前9项和是( )
| A、130 | B、170 |
| C、210 | D、260 |
如果(4x2-
)n的展开式中含有非零常数项,则正整数n的最小值为( )
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
 把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.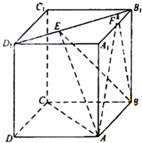 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有
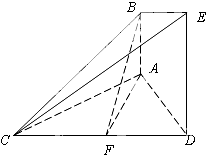 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.