题目内容
已知抛物线y2=2px过点M(
,
),A,B是抛物线上的点,直线OA,OM,OB的斜率成等比数列,则直线AB恒过定点 .
| 1 |
| 4 |
| ||
| 2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求出抛物线方程,再利用直线OA,OM,OB的斜率成等比数列,可得y1y2=
,求出直线方程令y=0,可得直线AB恒过定点(-
,0).
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:∵抛物线y2=2px过点M(
,
),
∴p=1,
∴抛物线方程为y2=2x,
设A(
,y1),B(
,y2),则
∵直线OA,OM,OB的斜率成等比数列,
∴8=
•
,
∴y1y2=
,
直线AB的方程为y-y1=
(x-
),
令y=0,可得x=-
y1y2=-
,
∴直线AB恒过定点(-
,0).
故答案为:(-
,0).
| 1 |
| 4 |
| ||
| 2 |
∴p=1,
∴抛物线方程为y2=2x,
设A(
| y12 |
| 2 |
| y22 |
| 2 |
∵直线OA,OM,OB的斜率成等比数列,
∴8=
| 2 |
| y1 |
| 2 |
| y2 |
∴y1y2=
| 1 |
| 2 |
直线AB的方程为y-y1=
| 2 |
| y2+y1 |
| y12 |
| 2 |
令y=0,可得x=-
| 1 |
| 2 |
| 1 |
| 4 |
∴直线AB恒过定点(-
| 1 |
| 4 |
故答案为:(-
| 1 |
| 4 |
点评:本题考查抛物线方程,考查直线恒过定点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设a=lg3,b=(lg3)2,c=lg
,则有( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、b>c>a |
| D、b>a>c |
如果(4x2-
)n的展开式中含有非零常数项,则正整数n的最小值为( )
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
函数y=(a2-4a+4)ax是指数函数,则a的值是( )
| A、4 | B、1或3 | C、3 | D、1 |
 把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.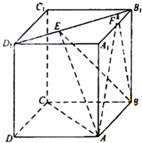 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有