题目内容
已知实数a,b满足ab=1,且a>b≥
,则
的最大值为 .
| 2 |
| 3 |
| a-b |
| a2+b2 |
考点:有理数指数幂的化简求值
专题:计算题,不等式的解法及应用
分析:由题意,化简
=
=
,求出a-b的取值范围,从而求
的最大值.
| a-b |
| a2+b2 |
| a-b |
| (a-b)2+2ab |
| 1 | ||
(a-b)+
|
| a-b |
| a2+b2 |
解答:
解:由题意,
=
,
∵ab=1,a>b≥
,
∴0<a-b≤
-
=
,
∴
=
=
,
∵y=x+
在(0,
)上是减函数,
∴
≤
=
.
故答案为:
.
| a-b |
| a2+b2 |
| a-b |
| (a-b)2+2ab |
∵ab=1,a>b≥
| 2 |
| 3 |
∴0<a-b≤
| 3 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
∴
| a-b |
| (a-b)2+2ab |
| a-b |
| (a-b)2+2 |
=
| 1 | ||
(a-b)+
|
∵y=x+
| 2 |
| x |
| 2 |
∴
| 1 | ||
(a-b)+
|
| 1 | ||||||
|
| 30 |
| 97 |
故答案为:
| 30 |
| 97 |
点评:本题考查了基本不等式的应用,注意0<a-b≤
,故
不能用基本不等式求最值,转到单调性求最值,属于中档题.
| 5 |
| 6 |
| 1 | ||
(a-b)+
|

练习册系列答案
相关题目
设0<a<1,m=loga(a2+1),n=loga(a+1),p=logaa,则m,n,p的大小关系是( )
| A、n>m>p |
| B、m>p>n |
| C、m>n>p |
| D、p>m>n |
实数x、y满足不等式组
,且z=ax+y(a>0)取最小值的最优解有无穷多个,则实数a的取值是( )
|
A、-
| ||
| B、1 | ||
| C、2 | ||
| D、无法确定 |
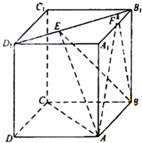 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,则下列结论中正确的有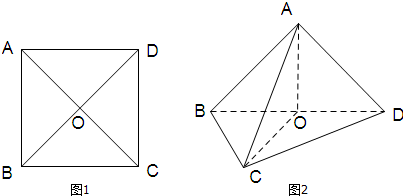
 设地球半径为R,北纬30°圈上有A,B两地,它们的经度相差120°,则这两地间的纬度线的长为
设地球半径为R,北纬30°圈上有A,B两地,它们的经度相差120°,则这两地间的纬度线的长为