题目内容
8．一个几何体的三视图如图所示（单位：cm），则该几何体的表面积是（ ）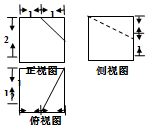
| A． | 4cm2 | B． | $\frac{43}{2}$cm2 | C． | 23cm2 | D． | 24cm2 |
分析 由三视图知该几何体是一个正方体截去一个三棱锥所得的组合体，累加各个面的面积，可求出几何体的表面积；
解答 解：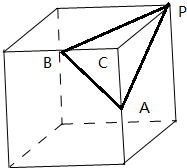
根据三视图可知几何体是：
一个正方体截去一个三棱锥P-ABC所得的组合体，
直观图如图所示：其中A、B是棱的中点，
正方体的棱长是2cm，则PA=PB=$\sqrt{5}$cm，AB=$\sqrt{2}$cm，
∴△PAB边AB上的高线为$\sqrt{{\sqrt{5}}^{2}-（\frac{\sqrt{2}}{2}）^{2}}$=$\frac{3\sqrt{2}}{2}$（cm），
∴该几何体的表面积：
S=6×2×2-2×$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×1+$\frac{1}{2}$×$\sqrt{2}$×$\frac{3\sqrt{2}}{2}$=23（cm2），
故选：C
点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
18．已知定义在R上的函数f（x）满足f（x）=f（-x），且当x∈（-∞，0）时，f（x）+xf'（x）＜0成立，若a=（20.1）•f（20.1），b=（ln2）•f（ln2），$c=（{log_2}\frac{1}{8}）•f（{log_2}\frac{1}{8}）$，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | c＞b＞a | C． | c＜a＜b | D． | a＞c＞b |
19．定义函数序列：${f_1}（x）=f（x）=\frac{x}{1-x}$，f2（x）=f（f1（x）），f3（x）=f（f2（x）），…，fn（x）=f（fn-1（x）），则函数y=f2017（x）的图象与曲线$y=\frac{1}{x-2017}$的交点坐标为（ ）
| A． | $（{-1，-\frac{1}{2018}}）$ | B． | $（{0，\frac{1}{-2017}}）$ | C． | $（{1，\frac{1}{-2016}}）$ | D． | $（{2，\frac{1}{-2015}}）$ |
16．在区间[0，1]上任取两个实数a，b，则函数f（x）=x2+ax+b2无零点的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
3．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的离心率是（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{5}{3}$ | C． | $\frac{{\sqrt{7}}}{4}$ | D． | $\frac{25}{16}$ |
某四面体的三视图如图所示，则此四面体的四个面中面积最大的面的面积等于$2\sqrt{3}$．
20．集合 A={x|-1＜x＜1}，B={x|x（x-2）＞0}，那么 A∩B=（ ）
| A． | {x|-1＜x＜0} | B． | {x|-1＜x＜2} | C． | {x|0＜x＜1} | D． | {x|x＜0或x＞2} |