题目内容
19.定义函数序列:${f_1}(x)=f(x)=\frac{x}{1-x}$,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn-1(x)),则函数y=f2017(x)的图象与曲线$y=\frac{1}{x-2017}$的交点坐标为( )| A. | $({-1,-\frac{1}{2018}})$ | B. | $({0,\frac{1}{-2017}})$ | C. | $({1,\frac{1}{-2016}})$ | D. | $({2,\frac{1}{-2015}})$ |
分析 由题意,可先求出f1(x),f2(x),f3(x)…,归纳出fn(x)的表达式,即可得出f2017(x)的表达式,进而得到答案.
解答 解:由题意f1(x)=f(x)=$\frac{x}{1-x}$.
f2(x)=f(f1(x))=$\frac{\frac{x}{1-x}}{1-\frac{x}{1-x}}$=$\frac{x}{1-2x}$,
f3(x)=f(f2(x))=$\frac{\frac{x}{1-2x}}{1-\frac{x}{1-2x}}$=$\frac{x}{1-3x}$,
…
fn(x)=f(fn-1(x))=$\frac{x}{1-nx}$,
∴f2017(x)=$\frac{x}{1-2017x}$,
由$\left\{\begin{array}{l}y=\frac{1}{x-2017}\\ y=\frac{x}{1-2017x}\end{array}\right.$得:$\left\{\begin{array}{l}x=1\\ y=\frac{1}{-2016}\end{array}\right.$,或$\left\{\begin{array}{l}x=-1\\ y=\frac{1}{-2018}\end{array}\right.$,
由${f_1}(x)=f(x)=\frac{x}{1-x}$中x≠1得:
函数y=f2017(x)的图象与曲线$y=\frac{1}{x-2017}$的交点坐标为$({-1,-\frac{1}{2018}})$,
故选:A
点评 本题考查逻辑推理中归纳推理,由特殊到一般进行归纳得出结论是此类推理方法的重要特征.

练习册系列答案
相关题目
14.已知直线l1:3x+2y+1=0,l2:x-2y-5=0,设直线l1,l2的交点为A,则点A到直线${l_0}:y=-\frac{3}{4}x-\frac{5}{2}$的距离为( )
| A. | 1 | B. | 3 | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\frac{{15\sqrt{7}}}{7}$ |
11.直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于( )
| A. | 20π | B. | 10π | C. | 5π | D. | 5$\sqrt{5}$π |
8.一个几何体的三视图如图所示(单位:cm),则该几何体的表面积是( )
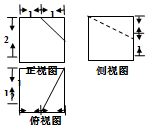

| A. | 4cm2 | B. | $\frac{43}{2}$cm2 | C. | 23cm2 | D. | 24cm2 |
9.若直线x+y+m=0与圆x2+y2=m相切,则m的值是( )
| A. | 0或2 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$或2 |