题目内容
16．在区间[0，1]上任取两个实数a，b，则函数f（x）=x2+ax+b2无零点的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
分析 函数f（x）=x2+ax+b2无零点的条件，得到a，b满足的条件，利用几何概型的概率公式求出对应的面积即可得到结论．
解答 解：∵a，b是区间[0，1]上的两个数，
∴a，b对应区域面积为1×1=1
若函数f（x）=x2+ax+b2无零点，
则△=a2-4b2＜0，对应的区域为直线a-2b=0的上方，
面积为1-$\frac{1}{2}×1×\frac{1}{2}$=$\frac{3}{4}$，
则根据几何概型的概率公式可得所求的概率为$\frac{3}{4}$．
故选：B．
点评 本题主要考查几何概型的概率计算，根据二次函数无零点的条件求出a，b满足的条件是解决本题的关键．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
6．下列四个命题中真命题为（ ）
| A． | lg（x2+1）≥0 | B． | 5≤2 | C． | 若x2=4，则x=2 | D． | 若x＜2，则$\frac{1}{x}$＞$\frac{1}{2}$ |
11．直三棱柱ABC-A1B1C1的各顶点都在同一球面上，若AB=AC=AA1=2，∠BAC=120°，则此球的表面积等于（ ）
| A． | 20π | B． | 10π | C． | 5π | D． | 5$\sqrt{5}$π |
1．
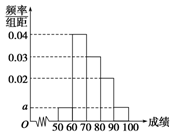某校100名学生期中考试语文成绩的频率分布直方图如下图所示，其中成绩分组区间是[50，60），[60，70），[70，80），[80，90），[90，100]．
（Ⅰ）求图中a的值；
（Ⅱ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．
某校100名学生期中考试语文成绩的频率分布直方图如下图所示，其中成绩分组区间是[50，60），[60，70），[70，80），[80，90），[90，100]．（Ⅰ）求图中a的值；
（Ⅱ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
8．一个几何体的三视图如图所示（单位：cm），则该几何体的表面积是（ ）
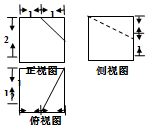
| A． | 4cm2 | B． | $\frac{43}{2}$cm2 | C． | 23cm2 | D． | 24cm2 |
5．过抛物线y2=4x的焦点作一条直线与抛物线相交于A，B两点，它们的横坐标之和等于3，则这样的直线（ ）
| A． | 有且仅有一条 | B． | 有且仅有两条 | C． | 有无穷多条 | D． | 不存在 |
6．函数y=ex（e是自然对数的底数）在点（0，1）处的切线方程是（ ）
| A． | y=x-1 | B． | y=x+1 | C． | y=-x-1 | D． | y=-x+1 |