题目内容
17.在△ABC所在平面内一点P,满足$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$,延长BP交AC于点D,若$\overrightarrow{AD}=λ\overrightarrow{AC}$,则λ=$\frac{1}{3}$.分析 用特殊值法,不妨设△ABC是等腰直角三角形,腰长AB=AC=1,建立直角坐标系,利用坐标法和向量共线,求出点D的坐标,即可得出λ的值.
解答 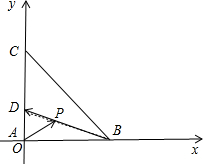 解:根据题意,不妨设△ABC是等腰直角三角形,
解:根据题意,不妨设△ABC是等腰直角三角形,
且腰长AB=AC=1,
建立直角坐标系,如图所示,
则A(0,0),B(1,0),C(0,1),
∴$\overrightarrow{AB}$=(1,0),$\overrightarrow{AC}$=(0,1);
∴$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$=($\frac{2}{5}$,$\frac{1}{5}$),
∴$\overrightarrow{BP}$=$\overrightarrow{AP}$-$\overrightarrow{AB}$=(-$\frac{3}{5}$,$\frac{1}{5}$);
设点D(0,y),
则$\overrightarrow{BD}$=(-1,y),
由$\overrightarrow{BP}$、$\overrightarrow{BD}$共线,得y=$\frac{1}{3}$,
∴$\overrightarrow{AD}$=(0,$\frac{1}{3}$),$\overrightarrow{AC}$=(0,1),
当$\overrightarrow{AD}=λ\overrightarrow{AC}$时,
λ=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查平面向量的基本定理及其意义,也考查了转化思想与运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个几何体的三视图如图所示(单位:cm),则该几何体的表面积是( )
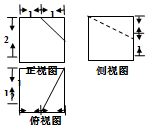

| A. | 4cm2 | B. | $\frac{43}{2}$cm2 | C. | 23cm2 | D. | 24cm2 |
5.过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们的横坐标之和等于3,则这样的直线( )
| A. | 有且仅有一条 | B. | 有且仅有两条 | C. | 有无穷多条 | D. | 不存在 |
12.“k=1”是“直线$kx-y-3\sqrt{2}=0$与圆x2+y2=9相切”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.△ABC是球的一个截面的内接三角形,其中AB=18,BC=24、AC=30,球心到这个截面的距离为球半径的一半,则球的半径等于( )
| A. | 10 | B. | $10\sqrt{3}$ | C. | 15 | D. | $15\sqrt{3}$ |
9.若直线x+y+m=0与圆x2+y2=m相切,则m的值是( )
| A. | 0或2 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$或2 |
6.函数y=ex(e是自然对数的底数)在点(0,1)处的切线方程是( )
| A. | y=x-1 | B. | y=x+1 | C. | y=-x-1 | D. | y=-x+1 |
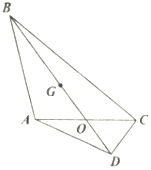 如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.