题目内容
已知数列{an}满足:a1=2t-3(t∈R且t≠±1),an+1=
(n∈N*)
(Ⅰ)证明数列{
}为等差数列,并求数列{an}的通项公式;
(Ⅱ)设bn=n2(an+1),求数列{bn}的前n项和Sn;
(Ⅲ)若t>0,证明数列{an}为单调递增数列.
| 2(tn+1-1)(an+1) |
| an+2tn-1 |
(Ⅰ)证明数列{
| tn-1 |
| an+1 |
(Ⅱ)设bn=n2(an+1),求数列{bn}的前n项和Sn;
(Ⅲ)若t>0,证明数列{an}为单调递增数列.
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(Ⅰ)由已知得
=
=
,由此能证明数列{
}是首项为
,公差为
的等差数列,从而求出an=
.
(Ⅱ)bn=n2(an+1)=2n(tn-1)=2ntn-2n,若t=0,则数列{bn}的前n项和Sn=-n(n+1);若t≠0,t≠±1,记数列{ntn}的前n 项和 为Tn,Tn=t+2t2+3t3+…+ntn,由错位相减法能求出数列{bn}的前n项和Sn.
(III)t>0,能推导出an+1-an>0,由此能证明数列{an}为单调递增数列.
| an+1+1 |
| tn+1-1 |
| 2(an+1) |
| an+2tn-1 |
| ||
|
| tn-1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2tn-n-2 |
| n |
(Ⅱ)bn=n2(an+1)=2n(tn-1)=2ntn-2n,若t=0,则数列{bn}的前n项和Sn=-n(n+1);若t≠0,t≠±1,记数列{ntn}的前n 项和 为Tn,Tn=t+2t2+3t3+…+ntn,由错位相减法能求出数列{bn}的前n项和Sn.
(III)t>0,能推导出an+1-an>0,由此能证明数列{an}为单调递增数列.
解答:
解:(Ⅰ)∵数列{an}满足:a1=2t-3(t∈R且t≠±1),
an+1=
(n∈N*),
∴
=
=
,…(2分)
记bn=
,则bn+1=
,b1=
=
=2,…(3分)
又
=
+
,
=
,
∴数列{
}是首项为
,公差为
的等差数列.…(4分)
∴
=
n,
∴an=
.…(5分)
(Ⅱ)bn=n2(an+1)=2n(tn-1)=2ntn-2n,…(6分)
若t=0,则数列{bn}的前n项和Sn=-n(n+1),…(7分)
若t≠0,t≠±1,记数列{ntn}的前n 项和 为Tn,
则Tn=t+2t2+3t3+…+ntn,
由错位相减得Tn=
-
,
从而Sn=
-
-n(n+1).…(10分)
(III)an+1-an=
-
=
[n(1+t+…+tn-1+tn)-(n+1)(1+t+…+tn-1)]
=
[ntn-(1+t+…+tn-1)]=
[(tn-1)+(tn-t)+…+(tn-tn-1)]
…(12分)
(1)若0<t<1,则t-1<0,tn-ti<0(i=0,1,…,n-1),从而an+1-an>0; …(13分)
(2)若t>1,则t-1>0,tn-ti>0(i=0,1,…,n-1),从而an+1-an>0.
综上知,对任意t>0,t≠1,数列{an}均为递增数列.…(14分)
an+1=
| 2(tn+1-1)(an+1) |
| an+2tn-1 |
∴
| an+1+1 |
| tn+1-1 |
| 2(an+1) |
| an+2tn-1 |
| ||
|
记bn=
| an+1 |
| tn-1 |
| 2bn |
| bn+2 |
| a1+1 |
| t-1 |
| 2t-2 |
| t-1 |
又
| 1 |
| bn+1 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| b1 |
| 1 |
| 2 |
∴数列{
| tn-1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| tn-1 |
| an+1 |
| 1 |
| 2 |
∴an=
| 2tn-n-2 |
| n |
(Ⅱ)bn=n2(an+1)=2n(tn-1)=2ntn-2n,…(6分)
若t=0,则数列{bn}的前n项和Sn=-n(n+1),…(7分)
若t≠0,t≠±1,记数列{ntn}的前n 项和 为Tn,
则Tn=t+2t2+3t3+…+ntn,
由错位相减得Tn=
| t(1-tn) |
| (1-t)2 |
| ntn+1 |
| 1-t |
从而Sn=
| 2t(1-tn) |
| (1-t)2 |
| 2ntn+1 |
| 1-t |
(III)an+1-an=
| 2(tn+1-1) |
| n+1 |
| 2(tn-1) |
| n |
| 2(t-1) |
| n(n+1) |
=
| 2(t-1) |
| n(n+1) |
| 2(t-1) |
| n(n+1) |
…(12分)
(1)若0<t<1,则t-1<0,tn-ti<0(i=0,1,…,n-1),从而an+1-an>0; …(13分)
(2)若t>1,则t-1>0,tn-ti>0(i=0,1,…,n-1),从而an+1-an>0.
综上知,对任意t>0,t≠1,数列{an}均为递增数列.…(14分)
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查数列是单调递增数列的证明,解题时要认真审题,注意作差法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
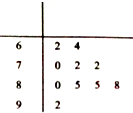 为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.
为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.