题目内容
某公司一年购买某种货物400吨，每次都购买x吨，运费为4万元/次，一年的总存储费为4x万元，一年的总运费与总存储费之和记为y（单位：万元）．
（1）将y表示为x的函数；
（2）当x为何值时，y取最小值？并求出y的最小值．
（1）将y表示为x的函数；
（2）当x为何值时，y取最小值？并求出y的最小值．
考点：函数模型的选择与应用
专题：函数的性质及应用,不等式的解法及应用
分析：（1）根据条件关系，即可求出y的函数关系；
（2）利用基本不等式的性质即可求出y取最小值？
（2）利用基本不等式的性质即可求出y取最小值？
解答：
解：（1）由题意知每年购买次数为
次，
则一年的总运费为
×4=
，
则y=
+4x，（x＞0）．
（2）由（1）得y=
+4x≥2
=160，
当且仅当
=4x，即x=20时等号成立，
故当x=20吨时，y取最小值160万元．
| 400 |
| x |
则一年的总运费为
| 400 |
| x |
| 1600 |
| x |
则y=
| 1600 |
| x |
（2）由（1）得y=
| 1600 |
| x |
|
当且仅当
| 1600 |
| x |
故当x=20吨时，y取最小值160万元．
点评：本题主要考查函数的应用问题，根据条件建立函数关系，利用基本不等式进行求解最值是解决本题的关键．
练习册系列答案
相关题目
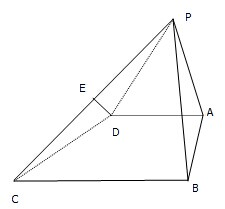如图所示，在四棱锥P-ABCD中，△PAB为正三角形，且面PAB⊥面ABCD，四边形ABCD为直角梯形，且AD∥BC，∠BCD=
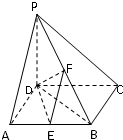如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是正方形，PD=DC，E、F分别为AB、PB的中点．