题目内容
已知p:直线x-y+m=0与圆x2+y2-2x-4y+3=0没有公共点.q:不等式x-
-m≥0对于任意x∈[2,3]恒成立.若p或q为真命题,p且q为假命题,求实数m的取值范围.
| 1 |
| x |
考点:复合命题的真假
专题:简易逻辑
分析:首先,求解给定命题为真命题时,相应的实数m的取值情况,然后,结合p或q为真命题,p且q为假命题,故得到:p和q一真一假,最后,分两种情形进行讨论,得到实数m的取值范围.
解答:
解:对于命题p:圆的方程可化为(x-1)2+(y-2)2=2其圆心为(1,2)半径为
.
故
>
解得m>3或m<-1.
对于命题q:分离得m≤x-
对x∈[2,3]恒成立,
由y=x-
在[2,3]上单调递增知道m≤
.
∵p或q为真命题,p且q为假命题,
∴p和q一真一假,
①当p真q假时,
即
,
解得m>3,
②当p假q真时,
得
,
解得-1≤m≤
,
∴所求m的取值范围是[-1,
]∪(3,+∞).
| 2 |
故
| |1-2+m| | ||
|
| 2 |
解得m>3或m<-1.
对于命题q:分离得m≤x-
| 1 |
| x |
由y=x-
| 1 |
| x |
| 3 |
| 2 |
∵p或q为真命题,p且q为假命题,
∴p和q一真一假,
①当p真q假时,
即
|
解得m>3,
②当p假q真时,
得
|
解得-1≤m≤
| 3 |
| 2 |
∴所求m的取值范围是[-1,
| 3 |
| 2 |
点评:本题综合考查了复合命题及其真假判断,分类讨论思想在求解简易逻辑问题中的应用,属于中档题.

练习册系列答案
相关题目
已知下列四个命题:
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
;
④4条棱均为
的四面体的体积是
;
其中真命题的序号是( )
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
| 1 |
| 4 |
④4条棱均为
| 2 |
| 1 |
| 3 |
其中真命题的序号是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
二次函数y=ax2+bx与指数函数y=(-
)x的图象只可能是( )
| b |
| a |
A、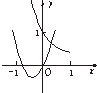 |
B、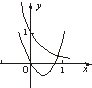 |
C、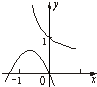 |
D、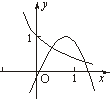 |