题目内容
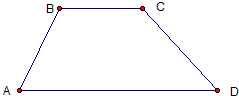如图，已知| AB |
| CD |
| BC |
（1）若四边形ABCD为梯形，求x、y间的函数的关系式；
（2）若以上梯形的对角线互相垂直，求
| BC |
考点：函数解析式的求解及常用方法,平面向量数量积的运算
专题：函数的性质及应用,平面向量及应用
分析：（1）由题意，梯形ABCD中，用
、
、
表示出
，由
与
共线，用坐标表示即可求出x、y的关系式；
（2）用坐标表示出对角线
、
，由
⊥
，得出
•
=0，即得方程x2+y2-x-2y-5=0①；又y=2x②；由①②解出
的坐标．
| AB |
| BC |
| CD |
| AD |
| BC |
| AD |
（2）用坐标表示出对角线
| AC |
| BD |
| AC |
| BD |
| AC |
| BD |
| BC |
解答：
解：（1）
=
+
+
=(x-1，y-2)，
∵
与
不共线，四边形ABCD为梯形，
∴
与
共线；
∴y（x-1）-x（y-2）=0，
∴y=2x．
（2）
=
+
=（x+1，y+1），
=
+
=（x-2，y-3），
⊥
，
∴
•
=0；
∴（x+1）（x-2）+（y+1）（y-3）=0，
即x2+y2-x-2y-5=0①；
又y=2x②，
由①②得，
或
；
∴
=（
，1+
）或（
，1-
）．
| AD |
| AB |
| BC |
| CD |
∵
| AB |
| CD |
∴
| BC |
| AD |
∴y（x-1）-x（y-2）=0，
∴y=2x．
（2）
| AC |
| AB |
| BC |
| BD |
| BC |
| CD |
| AC |
| BD |
∴
| AC |
| BD |
∴（x+1）（x-2）+（y+1）（y-3）=0，
即x2+y2-x-2y-5=0①；
又y=2x②，
由①②得，
|
|
∴
| BC |
1+
| ||
| 2 |
| 5 |
1-
| ||
| 2 |
| 5 |
点评：本题考查了利用向量的坐标表示求函数的解析式以及向量的数量积的应用问题，解题时应根据向量的坐标运算，结合图形，进行计算，是综合题目．
练习册系列答案
名校课堂系列答案
相关题目
已知f（x）=6cos2