题目内容
5．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-4≤0}\\{（x-2）^{2}+{y}^{2}≤4}\end{array}\right.$，则z=-$\frac{\sqrt{3}}{3}$x+y的最小值为（ ）| A． | -2$\sqrt{3}$ | B． | -$\sqrt{3}$ | C． | 0 | D． | $\frac{2\sqrt{3}}{3}$ |
分析 作出平面区域，移动目标函数，观察图形寻找最优解的位置．
解答 解：作出平面区域如图：
由z=-$\frac{\sqrt{3}}{3}$x+y得y=$\frac{\sqrt{3}}{3}$x+z，
由图可知当y=$\frac{\sqrt{3}}{3}$x+z与圆（x-2）2+y2=4相切时，z取得最小值．
把y=$\frac{\sqrt{3}}{3}$x+z化成一般式方程为$\sqrt{3}$x-3y+3z=0，
∴$\frac{|2\sqrt{3}+3z|}{\sqrt{3+9}}$=2，解得z=-2$\sqrt{3}$或z=$\frac{2\sqrt{3}}{3}$（舍）．
故选：A．
点评 本题考查了简单的线性规划，作出平面区域寻找最优解的位置是解题关键．
练习册系列答案
相关题目
15．直线a∥平面α，直线b⊥平面α，则下列说法正确的是（ ）
| A． | a∥b | B． | a⊥b | C． | a⊥b且异面 | D． | a⊥b且相交 |
16．某产品的广告费用支出x与销售额y（单位：百万元）之间有如下的对应数据：
（1）求y与x之间的回归直线方程；（参考数据：22+42+52+62+82=145，2×30+4×40+5×60+6×50+8×70=1380）
（2）试预测广告费用支出为1千万元时，销售额是多少？
附：线性回归方程y=bx+a中，b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$，其中$\overline{x}$，$\overline{y}$为样本平均值，线性回归方程也可写为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$．
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
（2）试预测广告费用支出为1千万元时，销售额是多少？
附：线性回归方程y=bx+a中，b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$，其中$\overline{x}$，$\overline{y}$为样本平均值，线性回归方程也可写为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$．
20．下列判断中错误的是（ ）
| A． | 角α确定时，它在单位圆中的正弦线确定 | |
| B． | 单位圆中有相同正弦线的角相等 | |
| C． | 角α和角α+π具有相同的正切线 | |
| D． | 单位圆中有相同正切线的角的终边在同一直线上 |
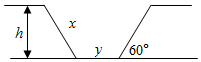某地兴修水利开建一条水渠，其断面为等腰梯形，腰与水平线的夹角为60°，要求湿透周长（即断面与水接触的边界长度）为定值l．问渠深h为多少时，可使水流量最大？最大水流量是多少？