题目内容
13.已知点G是△ABC的重心,在线段AC上取一点E,在线段AB上取一点F,若EF过G.求证:$\frac{|BF|}{|FA|}$+$\frac{|CE|}{|EA|}$=1.分析 根据题意画出图形,结合图形,设$\frac{\overrightarrow{BF}}{\overrightarrow{FA}}$=λ,$\frac{\overrightarrow{CE}}{\overrightarrow{EA}}$=μ,求出$\overrightarrow{AF}$=$\frac{1}{1+λ}$$\overrightarrow{AB}$,$\overrightarrow{AE}$=$\frac{1}{1+μ}$$\overrightarrow{AC}$;根据G是△ABC的重心,得出$\overrightarrow{AG}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$;
根据E、F、G三点共线,得出$\overrightarrow{AG}$=k$\overrightarrow{AE}$+(1-k)$\overrightarrow{AF}$,由此求出λ+μ的值.
解答 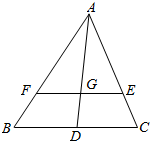 证明:如图所示,
证明:如图所示,
设$\frac{\overrightarrow{BF}}{\overrightarrow{FA}}$=λ,$\frac{\overrightarrow{CE}}{\overrightarrow{EA}}$=μ,
∴$\frac{\overrightarrow{BF}+\overrightarrow{FA}}{\overrightarrow{FA}}$=λ+1,即$\frac{\overrightarrow{BA}}{\overrightarrow{FA}}$=λ+1,
∴$\overrightarrow{FA}$=$\frac{1}{λ+1}$$\overrightarrow{BA}$,即$\overrightarrow{AF}$=$\frac{1}{1+λ}$$\overrightarrow{AB}$,
同理$\overrightarrow{AE}$=$\frac{1}{1+μ}$$\overrightarrow{AC}$;
又G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$;
又E、F、G三点共线,
设$\overrightarrow{AG}$=k$\overrightarrow{AE}$+(1-k)$\overrightarrow{AF}$,
则$\overrightarrow{AG}$=$\frac{k}{1+μ}$$\overrightarrow{AC}$+$\frac{1-k}{1+λ}$$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{1}{3}$$\overrightarrow{AB}$,
∴$\left\{\begin{array}{l}{\frac{k}{1+μ}=\frac{1}{3}}\\{\frac{1-k}{1+λ}=\frac{1}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{λ=2-3k}\\{μ=3k-1}\end{array}\right.$,
∴λ+μ=1,即$\frac{|BF|}{|FA|}$+$\frac{|CE|}{|EA|}$=1.
点评 本题考查了平面向量的线性表示与运算问题,也考查了定比分点与三点共线的应用问题,是中档题目.

| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
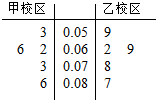 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )| A. | 甲校区较小 | B. | 乙校区较小 | ||
| C. | 甲乙两个校区相等 | D. | 无法确定 |
| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 0 | D. | $\frac{2\sqrt{3}}{3}$ |