题目内容
 在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,求证:
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,求证:(1)MN∥平面CC1D1D.
(2)平面MNP∥平面CC1D1D.
考点:平面与平面平行的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据线面平行的判定定理证明即可;(2)根据面面平行的判定定理证明即可.
解答:
证明:(1)连接AC,CD1,
∵ABCD是正方形,N是BD中点,
∴N是AC中点,
又∵M是AD1中点,
∴MN∥CD1,
∵MN?平面CC1D1D,CD1?平面CC1D1D,
∴MN∥平面CC1D1D;
(2)连接BC1,C1D,
∵B1BCC1是正方形,P是B1C的中点,
∴P是BC1中点,
又∵N是BD中点,
∴PN∥C1D,
∵PN?平面CC1D1D,CD1?平面CC1D1D,
∴PN∥平面CC1D1D,
由(1)得MN∥平面CC1D1D,且MN∩PN=N,
∴平面MNP∥平面面CC1D1D.
∵ABCD是正方形,N是BD中点,
∴N是AC中点,
又∵M是AD1中点,
∴MN∥CD1,
∵MN?平面CC1D1D,CD1?平面CC1D1D,
∴MN∥平面CC1D1D;
(2)连接BC1,C1D,
∵B1BCC1是正方形,P是B1C的中点,
∴P是BC1中点,
又∵N是BD中点,
∴PN∥C1D,
∵PN?平面CC1D1D,CD1?平面CC1D1D,
∴PN∥平面CC1D1D,
由(1)得MN∥平面CC1D1D,且MN∩PN=N,
∴平面MNP∥平面面CC1D1D.
点评:本题考查了线面平行,面面平行的判定定理,是一道中档题.

练习册系列答案
相关题目
函数f(x)=
的定义域是( )
| ||
| x-1 |
| A、{x|x≥4} |
| B、{x|x<4} |
| C、{x|x≤4,且x≠1} |
| D、{x|x<4,且x≠-1} |
定义在R上的函数f(x)的图象关于点(a,b),(c,b)都对称(a≠c),则( )
| A、f(x)是以|a-c|为周期的函数 | ||
| B、f(x)是以2|a-c|为周期的函数 | ||
C、f(x)是以
| ||
| D、f(x)不是周期函数 |
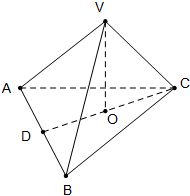 如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB=
如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB=