Question

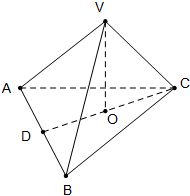如图，在三棱锥V-ABC中，VO⊥平面ABC，O∈CD，VA=VB=3

2

，AD=BD=3，BC=5．
（1）求证：VC⊥AB；
（2）当二面角∠VDC=60°时，求三棱锥V-ABC的体积．

Answer 1

考点：直线与平面垂直的性质,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）结合线面垂直的判定定理，从而证明线线垂直；（2）只需求出VO，CD的长，从而求出四面体的体积．

解答： （1）证明：连接VD，∵AD=BD=3，∴D是AB中点，
∵VA=VB=3

2

，∴VD⊥AB，
∵VO⊥平面ABC，∴AB⊥VO，
又VD∩VO=V，
∴VC⊥AB；
（2）在RT△VAD中，VA=3

2

，AD=3，∴VD=3，
在RT△VDO中，∠VDC=60°，VD=3，∴VO=

3

2

3

，
在RT△BCD中，BD=3，BC=5，∴CD=4，
∴V_V-ABC=

1

3

×

1

2

×6×4×

3

2

3

=6

3

．

点评：本题考查了线面垂直的判定定理，考查了椎体的体积，是一道基础题．