题目内容
一块各面均涂有油漆的正方体被锯成1000个小的正方体,若将这些小正方体均匀搅拌在一起,则任意取出的一个小正方体其两面均涂有油漆的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:
分析:由一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体,可得基本事件的总数有1000个,然后计算出满足条件两面有油漆的基本事件个数,代入率公式即可得到结果.
解答:
解:有题意知本题是一个等可能事件的概率,
一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体,
其中满足两面漆有油漆的小正方体有12×8=96个
∴从中随机地取出一个小正方体,其两面漆有油漆的概率P=
=
故选B.
一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体,
其中满足两面漆有油漆的小正方体有12×8=96个
∴从中随机地取出一个小正方体,其两面漆有油漆的概率P=
| 96 |
| 1000 |
| 12 |
| 125 |
故选B.
点评:本题考查等可能事件的概率,解题的关键是棱柱的结构特征,需要根据正方体共有12条棱,计算出两面漆有油漆的基本事件个数.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
|
| A、(0,2016) |
| B、(0,2016] |
| C、(0,504) |
| D、(0,504] |
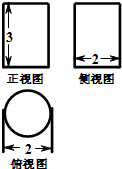 如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )
如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )| A、7π | B、8π |
| C、10π | D、π+12 |
给出如下性质:①最小正周期为π;②图象关于直线x=
对称;③在(-
,
)上是增函数.则同时具有上述性质的一个函数是( )
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
A、y=sin(
| ||||
B、y=cos(
| ||||
C、y=sin(2x-
| ||||
D、y=cos(2x+
|
不等式(x+1)(3-x)<0的解集是( )
| A、(-1,3) |
| B、(-∞,-1)∪(3,+∞) |
| C、(-3,1) |
| D、(-∞,-3)∪(1,+∞) |




