题目内容
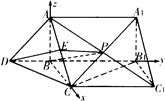
 直三棱柱ABC-A1B1C1中,AB⊥BC,BC=
直三棱柱ABC-A1B1C1中,AB⊥BC,BC=| 2 |
(Ⅰ)若AB=1,求证:BP∥平面ACD,
(Ⅱ)若直线CA1与平面BCC1B1所成的角为30°,求二面角D-AC-C1的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AC的中点E,连接PE,DE,证明四边形DBPE为平行四边形,从而BP∥平面ACD;
(Ⅱ)轴建立空间直角坐标系,用向量法解决.空间直角坐标系
(Ⅱ)轴建立空间直角坐标系,用向量法解决.空间直角坐标系
解答:
 (Ⅰ)证明:取AC的中点E,连接PE,DE…1分
(Ⅰ)证明:取AC的中点E,连接PE,DE…1分
则PE
CC1,∵BD=AB=1,BB1=2,∴BD=
BB1=
CC1,又∵BD∥CC1,∴BD
CC1,∴PE
BD,∴四边形DBPE为平行四边形,∴BP∥DE,…3分
∵BP?面ACD,DE?面ACD,…4分
∴BP∥平面ACD,…5分
(Ⅱ)解:由题意知,AB⊥BC,AB⊥BB1,∴AB⊥面BC1,∴A1B1⊥面BC1连接B1C,则∠A1CB1为直线CA1与平面BCC1B1所成的角,则∠A1CB1=30°,…6分
在Rt△A1B1C中,B1C=
=
,tanA1CB1
=
=
.∴A1B1=
…7分
以B为原点,分别以BC,BB1,AA1为x、y、z轴建立如图所示的
空间直角坐标系,则A(0,0,
),C(
,0,0),D(0,-
,0),
∴
=(
,0,-
),
=(0,-
,-
),…8分
设面ACD的法向量为
=(x,y,z),则
即
,取z=1,则
=(1,-1,1)…9分
在平面ABC内取面AC1的一个法向量
=(x,0,z),则
•
=
x-
z=0,取x=1,则z=1,∴
=(1,0,1)…10分
∴cos<
,
>=
=
,…11分
由图知二面角D-AC-C1为钝角,二面角D-AC-C1的余弦值为-
…12分
 (Ⅰ)证明:取AC的中点E,连接PE,DE…1分
(Ⅰ)证明:取AC的中点E,连接PE,DE…1分则PE
| ∥ |
. |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∵BP?面ACD,DE?面ACD,…4分
∴BP∥平面ACD,…5分
(Ⅱ)解:由题意知,AB⊥BC,AB⊥BB1,∴AB⊥面BC1,∴A1B1⊥面BC1连接B1C,则∠A1CB1为直线CA1与平面BCC1B1所成的角,则∠A1CB1=30°,…6分
在Rt△A1B1C中,B1C=
| 4+2 |
| 6 |
| A1B1 |
| B1C |
| A1B1 | ||
|
| ||
| 3 |
| 2 |
以B为原点,分别以BC,BB1,AA1为x、y、z轴建立如图所示的
空间直角坐标系,则A(0,0,
| 2 |
| 2 |
| 2 |
∴
| AC |
| 2 |
| 2 |
| AD |
| 2 |
| 2 |
设面ACD的法向量为
| n1 |
|
|
| n1 |
在平面ABC内取面AC1的一个法向量
| n2 |
| n2 |
| AC |
| 2 |
| 2 |
| n2 |
∴cos<
| n1 |
| n2 |
| 2 | ||||
|
| ||
| 3 |
由图知二面角D-AC-C1为钝角,二面角D-AC-C1的余弦值为-
| ||
| 3 |
点评:本题考查线面平行,考查面面角,考查向量知识的运用,解题的关键是正确建立坐标系,属于中档题.

练习册系列答案
相关题目
 如图,圆周上有n个固定点,分别为A1,A2,…,An(n∈N*,n≥2),在每一个点上分别标上1,2,3中的某一个数字,但相邻的两个数字不相同,记所有的标法总数为an.
如图,圆周上有n个固定点,分别为A1,A2,…,An(n∈N*,n≥2),在每一个点上分别标上1,2,3中的某一个数字,但相邻的两个数字不相同,记所有的标法总数为an. 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,